| |
| |
| | | | Status: | Approved for completion
in 2018
|
|
Modern Mathematical Physics:
Strings and Gravity, Supersymmetry, Integrability |
Leaders: | A.P. Isaev
A.S. Sorin
S.O. Krivonos |
| Scientific leader: | A.T. Filippov |
Participating Countries and International organizations:
Australia, Austria, Armenia, Brazil, Bulgaria, Canada, CERN,
Czech Republic, France, Germany, Greece, Hungary, ICTP, India, Italy, Japan,
Norway, Poland, Romania, Russia, Serbia, Spain, Turkey, Ukraine, USA, United Kingdom.
Scientific Programme:
The main purpose of research in modern mathematical physics is the development of mathematical methods for solving
the most important problems of modern theoretical physics: clarifying the nature of fundamental interactions and their
symmetries, construction and study of effective field models arising in the theory of strings and other extended objects,
uncovering the geometric description of quantum symmetries and their spontaneous breaking in the framework of search for a
unified theory of all fundamental interactions, including quantum gravity.
Mathematical physics in recent years has been characterized by increasing interest in identifying and effective used of
integrability in various areas, and in applying powerful mathematical methods of quantum groups, supersymmetry and non-commutative
geometry to quantum theories of fundamental interactions as well as to classical models.
The main goals and tasks of the research within the theme include:
development of new mathematical methods for description of a variety of integrable models and their exact classical and quantum solutions;
analysis of a wide range of problems in the theory of superstrings and superbranes, including study of nonperturbative regimes in supersymmetric
gauge theories; development of a microscopic description of black holes and constructing cosmological models of the early Universe.
The decisive factor to solve the above problems is a crucial use of the mathematical methods of the theory of integrable systems, quantum
groups and noncommutative geometry as well as superspace techniques.
Expected main results in 2018:
- Studies of topology and geometry of the moduli spaces of special Bohr — Sommerfeld lagrangian cycles in algebraic varieties.
Construction of canonical Berry bundles on the moduli spaces of special Bohr — Sommerfeld lagrangian cycles in algebraic varieties.
Construction of holographic renormalization group flows related to SL(2,C) Toda chains. Analysis of the obtained RG flows in the framework
of the gauge/gravity duality. Construction of solutions without a horizon (boson stars) with anti de-Sitter and anisotropic asymptotics.
Analysis of the solutions in the holographic framework.
Construction of Kerr-Vaidya/ Kerr-Newman-Vaidya solutions with AdS asymptotics for the D=5 supergravity model. Study of local operators (two-point correlation functions)
for the constructed metrics via holography.
Application of the generalised Reshetikhin formula for the scalar products of the Bethe vectors to the problems of form-factor calculations of the local
operators in the quantum integrable models with high symmetry. Reduction of these quantities to the determinant forms and its application to the problem
of calculation of the correlation functions in the thermodynamic limits.
Construction of classical integrable systems on varieties of modules of the preprojective algebras and their applications to generalised KP
hierarchies. Construction of integrable deformed elliptic Calogero–Moser systems by means of the elliptic Dunkl operators. Construction of
eigenfunctions of the deformed Macdonald–Ruijsenaars systems by using the representation theory of the Ding–Iohara algebra.
Study of systems of oscillators, invariant with respect to deformations of Galilei algebra (which include most of noncompact simple
Lie algebras). Prove that for any of these algebras it is possible to make the equations of motion for a system of harmonic or Pais-Uhlenbeck
oscillators linear. Apply these results to particular algebras (including G2).
Study the N=4 supersymmetric mechanics of many particles on curved spaces: generalize the necessary conditions for supersymmetry, including
the WDVV equations, find the condition for acceptable potentials, solve them in particular cases.
It is planned to obtain exact solutions for quantum problem of harmonic oscillator on two-sheeted hyperboloid SO(3,1)/SO(3) in four coordinate
systems: spherical, polar-cylindrical, equidistant-cylindrical and equidistant, and to find the coefficients of inter-basis expansion between given
coordinate systems. It is also planned to find a full solution for classical problems of Kepler-Coulomb and harmonic oscillator on one-sheeted
hyperboloid SO(3,1)/SO(2,1), by solving the Hamilton-Jacobi equations, and constructing the trajectories of motion.
Study of compact objects in modified theories of gravity.
Development of new methods for processing and analysis of observational data from detectors of gravitational waves.
Development of the theory and applications of Heun’s functions in problems of mathematical physics and theory of gravity.
- The two-loop quantum calculations in N=(1,1) 6D supersymmetric Yang-Mills theory will be preformed in the harmonic superspace approach:
the question of UV divergences and finite contributions to the effective action will be elucidated. There will be constructed all independent invariants of
canonical dimension d=12 and the issue of their (as well as of higher-dimensional invariants) possible application for constructing 6D Born-Infeld theory
with the manifest N=(1,0) and hidden N=(1,1) 6D supersymmetries.
There will be constructed new SU(2|2) and SU(4|2) supersymmetric extensions of the Calogero-Moser type models as deformations of N=4 and
N=8 supersymmetric extensions, the issue of their integrability and relationships with the matrix models of string theory will be studied.
The study of 6D supergravity models in the off-shell N = (1; 0) and on-shell N = (1; 1) 6D harmonic superspaces will be started. The constraints of N = (1; 1) 6D
supergravity will be solved in terms of N = (1; 0) superfields.
Construction of superfield action for the many-particle systems with N=4 and N=8 deformed supersym-metries. Superfield formulation of sigma model with Wess-Zumino
term possessing the N=4 and N=8 deformed supersymmetries and describing the interaction of the spinning particle with an external gauge background.
Construction of models for spinning particles and superparticles using momentum twistors. Obtaining of transition amplitudes from the BFV-BRST path integral.
Definition of geometries described by N=4 supersymmetric quantum mechanical sigma models with a variety of dynamical, semi-dynamical and gauge supermultiplets.
Determination of the type of supercharges for different geometries.
Construction of new hairy black holes linked to charged scalar clouds in the Kerr-Newman space-time. Investigation of the near BPS spinning self-gravitating
Skyrmions. Construction of spinning black holes with the BPS Skyrme hair.
- It is planned to study various boundary effects (the Casimir effect for instance) in conformal theories, and their possible holographic duals in gravity
theories to comprehend the peculiarities of their strong coupling regime. To this end the Casimir energy will be derived in free conformal theories
with D=3,4,6 which obey the boundary conditions preserving conformal invariance at boundaries of various geometries. Specifically, in d=4 the calculation
will be performed for N=4 super Yang-Mills theory. The results will be used to choose among different holographic descriptions those reproducing the Casimir
energy for conformal theories with boundaries.
Vacuum fluctuations of spinor and vector fields in the lattice background of n-dimensional delta function potentials will be studied. Similar two-dimensional
systems have attached recent attention related to the description of dispersion forces between polarizable sheets, for example graphene layers. The research
demands the development of differential operator’s self-ajoint extensions, and spectral geometry, specifically, spectral zeta functions and heat-kernel
expansions in singular background or with singular potential.
By making use of the two-time temperature Green functions, the vacuum friction force between macroscopic bodies will be calculated with account of all
orders in the relative velocity of the bodies.
We plan to perform the phase space analysis of some realistic f(R)-gravity models. We also plan to calculate the cosmological perturbations in such kind of models.
Studying of scalar-tensor teleparallel gravity models and calculation of cosmological perturbations in such kind of models will be performed.
It is planned to study gravity model based on a nonlinear realization of affine and conformal groups. Study of the model’s quantum features and renormalization
properties in first and second perturbation theory order.
Study of Horndeski gravity model’s features.
Investigation of the mass-inflation phenomenon on Cauchy horizon of black holes depending on their electric and magnetic charges, angular momenta and presence
of hairs, both in Einstein gravity and in gravity theories with non-minimal coupling. Such investigation promotes our understanding of singularity issues in
solutions to gravity theories.
Investigation of the Horndeski models with Maxwell and Yang-Mills fields applied to black holes and cosmologies. In cosmologies such theories attracted a lot
of interest because the corresponding lagrangian degenerates on de Sitter background. Recently we have shown that the presence of such quasiattractor gives
rise to natural finite-time inflation in Friedmann cosmology with SU(2) Yang-Mills field. It is planned to continue our investigation of these models in
the first-order (Einstein-Palatini) formalism, when connection is treated as an independent variable. For a theories with non-minimal coupling of matter
to gravity there is no a priori reason considering the metric-compatible connection, which leads to diverse dynamical models with new solutions.
Exact Stephani solutions with variable spatial curvature will be studied, their possible impact on inflationary cosmology and general topological properties
will be investigated. Question of cosmological horizon in the Einstein-Straus vacuole model and Lemaitre-Tolman-Bondi model will be studied.
Prospects for the formation of structures in the inhomogeneous models will be examined, observable cosmological parameters will be evaluated and experimental
data will be fitted. The Stephani and 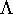 CDM cosmological models will be compared from the phenomenological point of view. CDM cosmological models will be compared from the phenomenological point of view.
Mannheim's conformal gravity will be analyzed, galactic rotation curves without presence of dark matter in light of up-to-date cosmological measurements will
be obtained. Internal structure of the Mannheim's theory, problems with unitarity, and its critical evaluation as a possible candidate for quantum gravity will be analyzed.
| List of Activities | | | Activity or experiment | Leaders | |
| | Laboratory or other
Division of JINR | Main researchers
|
| 1. | Quantum groups
and integrable systems | A.P. Isaev |
|
| |
BLTP
| P. Fiziev, J. Fuksa, A.A. Golubtsova, S.O. Krivonos, N.Yu. Kozyrev, V.K. Mitrjushkin, D.R. Petrosyan, G.S. Pogosyan,
A.V. Silantyev, N.A. Tyurin + 1 student
|
| 2. | Supersymmetry | E.A. Ivanov |
|
| |
BLTP
| S.A. Fedoruk, M. Pientek, A. Pietrikovsky, I.B. Samsonov, S.S. Sidorov, Ya.M. Shnir,
A.O.Sutulin
|
| 3. | Quantum gravity,
cosmology and strings | A.T. Filippov
V.V. Nesterenko
A.S. Sorin |
|
| |
BLTP
| B.M. Barbashov, I. Bormotova, E.A. Davydov, B.N. Latosh, A.B. Pestov, I.G. Pirozhenko,
E.A. Tagirov, P.V. Tretyakov, P. Yaluvkova + 3 students
|
| |
LIT
| I.L. Bogoliubsky, A.M. Chervyakov
|
| Collaboration |
Country or International
Organization | City | Institute or Laboratory |
| Armenia
| Yerevan
| YSU
|
|
| Australia
| Sydney
| Univ.
|
|
|
| Perth
| UWA
|
|
| Austria
| Vienna
| TU Wien
|
|
| Brazil
| Sao Paulo, SP
| USP
|
|
|
| Juiz de Fora, MG
| UFJF
|
|
| Bulgaria
| Sofia
| INRNE BAS
|
|
|
|
| SU
|
|
| Canada
| Montreal
| McGill
|
|
|
|
| UdeM
|
|
|
| Edmonton
| U of A
|
|
|
| Vancouver
| TRIUMF
|
|
| CERN
| Geneva
| CERN
|
|
| Czech Republic
| Opava
| SlU
|
|
|
| Prague
| CTU
|
|
|
|
| CU
|
|
|
| Rez
| NPI ASCR
|
|
| France
| Annecy-le-Vieux
| LAPP
|
|
|
| Dijon
| UB
|
|
|
|
| IMB
|
|
|
| Lyon
| ENS Lyon
|
|
|
| Marseille
| CPT
|
|
|
| Nantes
| SUBATECH
|
|
|
| Paris
| ENS
|
|
|
|
| LUTH
|
|
|
|
| LPTHE
|
|
|
| Palaiseau
| Polytech
|
|
|
| Valenciennes
| UVHC
|
|
| Germany
| Berlin
| FU Berlin
|
|
|
|
| MBI
|
|
|
| Bielefeld
| Univ.
|
|
|
| Bonn
| UniBonn
|
|
|
| Dortmund
| TU Dortmund
|
|
|
| Hannover
| LUH
|
|
|
| Jena
| Univ.
|
|
|
| Leipzig
| UoC
|
|
|
| Munich
| MPI-P
|
|
|
| Oldenburg
| IPO
|
|
|
| Potsdam
| AEI
|
|
| Greece
| Athens
| UoA
|
|
| Hungary
| Budapest
| Wigner RCP
|
|
| ICTP
| Trieste
| ICTP
|
|
| India
| Calcutta
| BNC
|
|
|
|
| IACS
|
|
|
| Chennai
| IMSc
|
|
| Italy
| Bari
| INFN
|
|
|
| Frascati
| INFN LNF
|
|
|
| Naples
| INFN
|
|
|
| Padua
| UniPd
|
|
|
| Pavia
| INFN
|
|
|
| Pisa
| INFN
|
|
|
| Salerno
| UNISA
|
|
|
| Trieste
| SISSA/ISAS
|
|
|
| Turin
| UniTo
|
|
| Japan
| Fukuoka
| Kyushu Univ.
|
|
|
| Kyoto
| KSU
|
|
|
|
| RIMS
|
|
|
|
| YITP
|
|
|
| Tsukuba
| KEK
|
|
|
| Fukusima
| Fukusima Univ.
|
|
|
| Tokyo
| UT
|
|
| Luxembourg
| Luxembourg
| Univ.
|
|
| Norway
| Trondheim
| NTNU
|
|
| Poland
| Warsaw
| NCAC PAS
|
|
|
|
| UW
|
|
|
| Krakow
| JU
|
|
|
|
| NINP PAS
|
|
|
| Lodz
| UL
|
|
|
| Wroclaw
| UW
|
|
| Romania
| Bucharest
| IFIN-HH
|
|
| Russia
| Moscow
| ITEP
|
|
|
|
| LPI RAS
|
|
|
|
| MSU
|
|
|
|
| MI RAS
|
|
|
|
| NRU HSE
|
|
|
|
| VNIIMS
|
|
|
|
| PFUR
|
|
|
|
| SAI MSU
|
|
|
| Moscow, Troitsk
| INR RAS
|
|
|
| Chernogolovka
| LITP RAS
|
|
|
| Dolgoprudny
| MIPT
|
|
|
| Kazan
| KFU
|
|
|
| Novosibirsk
| NSU
|
|
|
| Protvino
| IHEP
|
|
|
| St. Petersburg
| PDMI RAS
|
|
|
|
| SPbSU
|
|
|
| Tomsk
| TPU
|
|
|
|
| TSPU
|
|
| Serbia
| Belgrade
| IPB
|
|
|
|
| Univ.
|
|
| Spain
| Bilbao
| UPV/EHU
|
|
|
| Barcelona
| IEEC-CSIC
|
|
|
| Valencia
| IFIC
|
|
|
| Madrid
| ETSIAE
|
|
| Turkey
| Istanbul
| BU
|
|
|
| Izmir
| IZTECH
|
|
| Ukraine
| Kiev
| BITP NASU
|
|
|
| Kharkov
| NSC KIPT
|
|
| United Kingdom
| London
| Imperial College
|
|
|
| Cambridge
| Univ.
|
|
|
| Durham
| Univ.
|
|
|
| Liverpool
| Univ.
|
|
|
| Southampton
| Univ.
|
|
|
| York
| Univ.
|
|
|
| Glasgow
| U of G
|
|
|
| Leeds
| UL
|
|
|
| Brighton
| US
|
|
| USA
| New York, NY
| CUNY
|
|
|
|
| RU
|
|
|
|
| SUNY
|
|
|
| Cincinnati, OH
| UC
|
|
|
| College Park, MD
| UMD
|
|
|
| Coral Gables, FL
| UM
|
|
|
| Minneapolis, MN
| U of M
|
|
|
| Norman, OK
| OU
|
|
|
| Philadelphia, PA
| Penn
|
|
|
| Piscataway, NJ
| Rutgers
|
|
|
| Rochester, NY
| UR
|
|
|
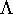 CDM cosmological models will be compared from the phenomenological point of view.
CDM cosmological models will be compared from the phenomenological point of view.