Содержание:
- Введение
- Построение модели сетки процессов
- Ввод данных в необходимые области
- Обращение к подпрограмме
- Компиляция, запуск и получение результатов
- Подпрограммы библиотеки ScaLAPACK
- Литература
- Приложение A: Пример решения системы уравнений с трехдиагональной матрицей
- Приложение B: Перечень подпрограмм пакета ScaLAPACK
- Простейшие примеры вызова программ (zip)
Введение
Библиотека с открытым исходным кодом ScaLAPACK (Scalable Linear Algebra Package) [1] является версией библиотеки LAPACK [2] для параллельных вычислений. Она содержит подпрограммы решения систем линейных уравнений, обращения матриц, нахождения собственных значений и собственных векторов и др. Библиотека написана на языке Fortran 77 (за исключением нескольких подпрограмм симметричных проблем на собственные значения, написанных на языке C) и ориентирована на работу в системах с архитектурой MIMD (Multiple Instruction stream, Multiple Data stream) и программным обеспечением PVM (Parallel Virtual Machine) [3] и/или MPI (Message Passing Interface) [4].
ScaLAPACK относится к числу параллельных библиотек, при обращении к которым пользователю не приходится явно применять какие - либо конструкции специальных языков параллельного программирования или интерфейсов, поддерживающих взаимодействие параллельных процессов. Все необходимые действия "по распараллеливанию" выполняются подпрограммами из специально разработанных для этих целей пакетов.
В библиотеке ScaLAPACK можно выделить локальные и глобальные компоненты (рис.1). К локальным компонентам относятся пакеты LAPACK (Linear Algebra Package) [2], BLAS (Basic Linear Algebra Subprograms) [5], BLACS (Basic Linear Algebra Communication Subprograms) [6]. Эти компоненты ориентированы на работу в однопроцессорном режиме. К глобальным компонентам относится параллельный вариант пакета BLAS — пакет PBLAS (Parallel BLAS) [7].
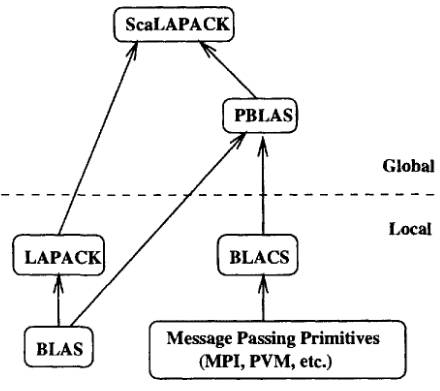
Рис. 1. Иерархия библиотеки ScaLAPACK
Библиотека LAPACK содержит последовательные подпрограммы линейной алгебры, оптимизированные для разнообразных процессоров, и в однопроцессорном режиме решает задачи обращения матриц, нахождения собственных векторов и собственных значений и др. Для повышения эффективности промежуточных операций умножения матрица-матрица используется библиотека BLAS, которая также ориентирована на работу на одиночных процессорах. Пакет PBLAS выполняет эти операции в распределенной памяти в параллельном виде. Особо примечателен пакет BLACS. Эта библиотека основана на модели одно- или двумерной сетки вычислительных процессов, где каждый процесс имеет дело только со своим фрагментом матрицы или вектора и занимается пересылкой/приемом данных между этими процессами с помощью соответствующего программного пакета (PVM и/или MPI).
Для работы с библиотекой программ ScaLAPACK пользователю необходимо выполнить следующие действия:
2. ввод данных в необходимые области;
3. обращение к нужной подпрограмме для решения задачи;
4. компиляция, запуск и получение результатов.
Рассмотрим каждый шаг более подробно.
1. Построение модели сетки процессов
За построение модели сетки процессов полностью отвечает пакет BLACS. Этот пакет на основе заданного количества процессов и выбранных пользователем размера блоков распределяет области памяти под фрагменты матриц и векторов между процессами в этой сетке. Для построения такой сетки используются следующие подпрограммы из библиотеки BLACS:
CALL BLACS_GET(-1, 0, ICTXT)
CALL BLACS_GRIDINIT(ICTXT, 'Row-major', NPROW, NPCOL)
Как правило, выходной параметр IAM указывает на номер текущего процесса, а NPROCS — общее количество процессов. Второй параметр подпрограммы BLACS_GET указывает на порядок расположения процессов в модельной сетке. При его нулевом значении порядок принимается по умолчанию. 'Row-major' ('Column-major') или просто 'R' ('C') указывают на строчную (столбцевую) ориентированность разделения областей. Если входные параметры NPROW и NPCOL заданы в виде пары (2, 3), то после этих трех строк программы мы имеем сетку размером 2 на 3. В данном случае для решения задачи нам требуется количество процессов, кратное на 6.
Для того чтобы определить, в каком именно процессе находимся, используется следующая подпрограмма библиотеки BLACS:
В результате пара MYROW и MYCOL определит точку (текущий процесс) в сетке процессов. Полученную таким образом информацию о распределении области нужно использовать для ввода данных и манипулирования этими данными внутри пакета ScaLAPACK. Для этого эта информация помещается в целый одномерный массив (дескриптор) DESCA (или DESCB, если решается задача с правой частью) размерностью 9.
Пример: построить модель сетки процессов для решения систем линейных уравнений AX = B с заполненной квадратной матрицей A. С помощью подпрограммы DESCINIT пакета ScaLAPACK присвоим необходимые значения:
CALL DESCINIT(DESCB,N,NRHS,NB,NBRHS,RSRC,CSRC,ICTXT,MXLLDB,INFO)
Это эквивалентно следующим операторам присваивания:
| DESCA( 1 ) = 1 | DESCB( 1 ) = 1 |
| DESCA( 2 ) = ICTXT | DESCB( 2 ) = ICTXT |
| DESCA( 3 ) = M | DESCB( 3 ) = N |
| DESCA( 4 ) = N | DESCB( 4 ) = NRHS |
| DESCA( 5 ) = MB | DESCB( 5 ) = NB |
| DESCA( 6 ) = NB | DESCB( 6 ) = NBRHS |
| DESCA( 7 ) = RSRC | DESCB( 7 ) = RSRC |
| DESCA( 8 ) = CSRC | DESCB( 8 ) = CSRC |
| DESCA( 9 ) = MXLLDA | DESCB( 9 ) = MXLLDB |
Значения переменных:
N — число столбцов матрицы A системы (глобальный размер массива A);
MB — число строк блока в разбиении матрицы A;
NB — число столбцов блока в разбиении матрицы A;
NRHS — число столбцов матрицы B (число правых частей);
NBRHS — число столбцов в блоке в разбиении матрицы B;
RSRC, CSRC — начальная координата распределения матрицы по сетке;
MXLLDA — максимальный размер массива A, приходящийся на один процесс (локальный размер массива A);
MXLLDB — максимальный размер массива B, приходящийся на один процесс (локальный размер массива B).
2. Ввод данных в необходимые области
На рис.2 продемонстрирован способ распределения исходной матрицы размерностью 9х9 между процессами в сетке размерностью 2х3:

Рис. 2. Распределение элементов матрицы между процессами (сетка 2х3).
Правая часть будет распределена точно таким же способом. Для одномерной правой части уместно следующее распределение:
Приводим значения всех параметров, описанных выше, в рамках примера на рис.2: M = N = 9; MB = NB = 2; NRHS = 1; NBRHS = 1; RSRC = CSRC =0; MXLLDA = 5; MXLLDB = 5.
Все эти параметры определяются пользователем.
3. Обращение к подпрограмме
После построения модельной сетки процессов и распределения данных между процессами для решения задачи можно обращаться к соответствующей программе пакета ScaLAPACK:
IA,JA — индексы массива A(IA:IA+M-1,JA:JA+N-1);
IB,JB — индексы массива B(IB:IB+N-1,JB:JB+NRHS-1);
INFO — выходной параметр целого типа.
Параметры IA,JA,IB,JB чаще выбирают равными 1, тогда индексы массивов A и B, находящиеся в отдельных процессах, начинаются с (1,1). Если глобальные массивы выбраны в полном размере в соответствии с размером исходной матрицы, то эти индексы можно варьировать.
4. Компиляция, запуск и получение результатов
На вычислительной ферме ЦИВК библиотека ScaLAPACK и ее составляющие BLACS, BLAS и LAPACK собраны компилятором ifort версии 11.1 и размещены в директории
Пользовательская программа myprog.f, использующая программы из этой библиотеки с технологией MPI, может быть скомпилирована следующим образом:
lxpub01:~ > mpif77 -o myprog myprog.f $USRLIB/libscalapack.a \
$USRLIB/libblacsF77init.a $USRLIB/libblacs.a $USRLIB/libblacsF77init.a \
$USRLIB/liblapack.a $USRLIB/libblas.a /opt/openmpi/lib/libmpi.so -lnsl
Запуск полученной в результате компиляции программы myprog на кластере ЦИВК осуществляется следующим образом:
#PBS -q defq
#PBS -l walltime=00:05:00
#PBS -l cput=00:20:00
#PBS -l nodes=4
echo "========= begin =========="
cd $PBS_O_WORKDIR 2>&1
if test -x myprog ; then
mpiexec ./myprog 2>&1
else
echo "executable not found in "`pwd`
fi
echo "========= end ==========="
echo "done"
5. Подпрограммы библиотеки ScaLAPACK
Имена всех вычислительных подпрограмм совпадают с именами соответствующих подпрограмм из пакета LAPACK, с той лишь разницей, что в начале имени добавляется символ P, указывающий на то, что это параллельная версия. Соответственно, принцип формирования имен подпрограмм имеет ту же самую схему, что и в LAPACK. Согласно этой схеме имена подпрограмм библиотеки имеют вид PXYYZZZ. Символ X может принимать значения: S — для вычислений с одинарной точностью; D — для вычислений с двойной точностью; C — для вычислений с комплексными значениями и Z — для вычислений с комплексными значениями двойной точности.
Пара YY указывает вид матриц и принимает следующие значения:
DT — трехдиагональная общего вида (хорошо обусловленная);
GB — ленточная общего вида;
GE — общего вида (несимметричная, возможно прямоугольная);
GG —матрица общего вида, обобщенные задачи;
HE — эрмитова;
OR — ортогональная;
PB — симметричная или положительно определенная ленточная эрмитова матрица;
PO — симметричная или положительно определенная эрмитова матрица;
PT — симметричная или положительно определенная трехдиагональная эрмитова матрица;
ST — симметричная трехдиагональная;
SY — симметричная;
TR — треугольная (квазитреугольная);
TZ — трапециевидная;
UN — унитарная.
ZZZ указывает на вычислительные особенности с указанными матрицами. Например, PDGESVX означает: D — подпрограмма с двойной точностью; GE — используемая в подпрограмме матрица имеет общий вид (квадратичный или прямоугольный, несимметричный); SVX — решение плохо обусловленных систем уравнений (экспертный случай), если задается только SV, то имеется в виду решения хорошо обусловленных систем уравнений (простой случай).
Ниже приводится функциональная таблица пакета ScaLAPACK. В таблице обозначено: SPD — симметричная положительно определенная; GQR — обобщенное QR разложение; GRQ — обобщенное RQ разложение; BSPD — ленточная SPD; SVD — сингулярное разложение.
Решения систем уравнений AX = B:
| Матрица | пр. | экс. | факт. | реш. | обр. | оценка | итер.уточ. |
| Треугольная | + | + | + | + | |||
| SPD | + | + | + | + | + | + | + |
| SPD ленточная (BSPD) | + | + | + | ||||
| SPD 3х диагональная | + | + | + | ||||
| Общая | + | + | + | + | + | + | + |
| Общая ленточная | + | + | + | ||||
| Общая 3х диагональная | + | + | + | ||||
| Наименьших квадратов | + | + | + | ||||
| GQR | + | ||||||
| GRQ | + |
| Задача | пр. | экс. | редукция | решение |
| Симметричная | + | + | + | + |
| Общая | + | + | + | + |
| Обобщенная BSPD | + | + | + | |
| SVD | + | + |
Литература:
- L. S. Blackford, J. Choi, A. Cleary, J. Demmel, I. Dhillon, J. J. Dongarra, S. Hammarling, G. Henry, A. Petitet, K. Stanley, D. W. Walker, and R. C. Whaley, ScaLAPACK users' guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1997. Официальный сайт пакета ScaLAPACK: http://www.netlib.org/scalapack/
- E. Anderson, Z. Bai, C. Bischof, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. Mckenney, S. Ostrouchov, and D. Sorensen, LAPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, second ed., 1995. Официальный сайт пакета LAPACK: http://www.netlib.org/lapack/
- A. Geist, A. Beguelin, J. Dongarra, W. Jiang, R. Manchek, and V. Sunderam, PVM: Parallel Virtual Machine. A Users' Guide and Tutorial for Networked Parallel Computing, MIT Press, Cambridge, MA, 1994.
- M. P. I. Forum, MPI: a message passing interface standard, International Journal of Supercomputer Applications and High Performance Computing, 8 (1994), pp. 3-4. Special issue on MPI. Also available electronically, the URL is ftp://www.netlib.org/mpi/mpi-report.ps.
- J. J. Dongarra, J. Du Croz, I. S. Duff, and S. Hammarling, Algorithm 679: A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 1-17.
- J. Dongarra and R. Van de Geijn, Two dimensional basic linear algebra communication subprograms, Computer Science Dept. Technical Report CS-91-138, University of Tennessee, Knoxville, TN, 1991.
- J. Choi, J. Dongarra, S. Ostrouchov, A. Petitet, D. Walker, and R. C. Whaley, A proposal for a set of parallel basic linear algebra subprograms, Computer Science Dept. Technical Report CS-95-292, University of Tennessee, Knoxville, TN, MAY 1995.
- А.А.Букатов, В.Н.Дацюк, А.И.Жегуло. Программирование многопроцессорных вычислительных систем. Ростов-на-Дону: ЦВВР, 2003. Глава 14. Библиотека подпрограмм ScaLAPACK. http://www.ict.edu.ru/ft/003626/rsu_bukatov.pdf
Декомпозиция области трехдиагональной матрицы производится сеткой 1 на NPCOL или MPCOL на 1. Размерность дескрипторов может быть сокращена до 7.
PROGRAM TRID
DOUBLE PRECISION DL,D,DU,B,X,WORK,T,T1,T2,ONE
INTEGER DESCA(7),DESCB(7),DESCX(7)
ALLOCATABLE DL(:),D(:),DU(:),B(:),X(:),WORK(:),B0(:)
INCLUDE "mpif.h"
C Initialize the process grid
CALL BLACS_PINFO( IAM, NPROCS )
C Input parameters
ONE = 1D0
N = 1000000
NRHS = 1
NPROW = 1
NPCOL = NPROCS
NB = N/NPCOL
MB = MOD(N,NPCOL)
IF(IAM.EQ.0) NB = NB + MB
LW = 12*NPCOL+3*NB+10*NPCOL+4*NRHS
CALL BLACS_GET( 0, 0, ICTXT )
CALL BLACS_GRIDINIT( ICTXT,'R',NPROW, NPCOL ) ! Row-major
CALL BLACS_GRIDINFO( ICTXT, NPROW, NPCOL, MYROW, MYCOL )
IF( MYROW.GE.NPROW .OR. MYCOL.GE.NPCOL ) GO TO 9993
C Define arrays
ALLOCATE(DL(NB),D(NB),DU(NB),B(NB),B0(NB),X(NB),WORK(LW))
C Descriptors
DESCA(1) = 501
DESCA(2) = ICTXT
DESCA(3) = N
DESCA(4) = NB
DESCA(5) = 0
DESCA(6) = 0
DESCA(7) = 0
C
DESCB(1) = 502
DESCB(2) = ICTXT
DESCB(3) = N
DESCB(4) = NB
DESCB(5) = 0
DESCB(6) = NB
DESCB(7) = 0
C
INF=NB
CALL EXMPLS(N,NRHS,DL,D,DU,X,B,INF,1,NB,IAM,NPROCS)
C Call the ScaLAPACK routine for solving C*X=B
t1=MPI_WTIME()
CALL PDDTSV(N,NRHS,DL,D,DU,1,DESCA,B,1,DESCB,WORK,LW,INFO)
t2=MPI_WTIME()
t=t2-t1
IF (MYCOL.NE.0) CALL MPI_SEND(T,1,MPI_REAL,0,0,comm,ierr)
IF( MYCOL.EQ.0 ) THEN
OPEN(UNIT=6,FILE='OUTPUT',STATUS='UNKNOWN')
WRITE(6, FMT = 9999 )
WRITE(6, FMT = 9998 ) N, N, NB
WRITE(6, FMT = 9997 ) NPROW*NPCOL, NPROW, NPCOL
WRITE(6, FMT = 9996 ) INFO
WRITE(6,FMT=9995) MYCOL,T
T3=T
DO I=1,NPROCS-1
CALL MPI_RECV(T,1,MPI_REAL,I,0,comm,statusi,ierr)
T3=T3+T
WRITE(6,FMT=9995) I,T
ENDDO
WRITE(6,'(D10.3)') T3/NPROCS
CLOSE(6)
END IF
*
* RELEASE THE PROCESS GRID
* Free the BLACS context
*
CALL BLACS_GRIDEXIT( ICTXT )
*
* Exit the BLACS
*
CALL BLACS_EXIT( 0 )
*
9999 FORMAT( /'ScaLAPACK Solution of tridiagonal linear system' )
9998 FORMAT( /'Solving Cx=b where C is a ', I8, ' by ', I8,
$ ' matrix with a block size of ', I8 )
9997 FORMAT( 'Running on ', I3, ' processes, where the process',
$ ' grid is ', I3, ' by ', I3 )
9996 FORMAT( /'INFO code returned by PDDTSV = ', I3 )
9995 FORMAT( /'This is ',I2,' process. Time of calc. is ',
$ D10.3,' sec.')
9993 CONTINUE
STOP
END
C
SUBROUTINE EXMPLS(N,IM,U,D,R,X,B,INF,I1,I2,IAM,NPROCS)
IMPLICIT REAL*8(A-H,O-Z)
DIMENSION U(*),D(*),R(*),X(*),B(*)
*
MB = INF
DO 1 I=I1,I2
1 B(I)=2D0
IF(IAM.EQ.0) THEN
B(I1)=3D0
DO 2 I=1,MB
2 B(I2+I)=2D0
ENDIF
IF(IAM.EQ.NPROCS-1) B(I2)=1D0
DO 3 I=I1,I2
X(I)=1D0
U(I)=-1D0
R(I)=1D0
D(I)=2D0
3 CONTINUE
IF(IAM.EQ.0) THEN
DO 4 I=1,MB
X(I2+I)=1D0
U(I)=-1D0
R(I)=1D0
4 D(I)=2D0
ENDIF
INF=0 ! symmetric
RETURN
END
Результаты:
ScaLAPACK Solution of tridiagonal linear system
Solving Cx=b where C is a 1000000 by 1000000 matrix with a block size of 250000
Running on 4 processes, where the process grid is 1 by 4
INFO code returned by PDDTSV = 0
This is 0 process. Time of calc. is 0.685D-01 sec.
This is 1 process. Time of calc. is 0.685D-01 sec.
This is 2 process. Time of calc. is 0.685D-01 sec.
This is 3 process. Time of calc. is 0.685D-01 sec.
Приложение Б. Перечень подпрограмм пакета ScaLAPACK
Подпрограммы решения систем уравнений:
Тип матрицы Операция Одинарная точность Двойная точность
S C D Z
общая (частичная простой PSGESV PCGESV PDGESV PZGESV
перестановка) экспертный PSGESVX PCGESVX PDGESVX PZGESVX
общая ленточная простой PSGBSV PCGBSV PDGBSV PZGBSV
(част.перестановка)
общая ленточная простой PSDBSV PCDBSV PDDBSV PZDBSV
(без перестановки)
общая 3 диагональная простой PSDTSV PCDTSV PDDTSV PZDTSV
(без перестановки)
симмет./эрмитова простой PSPOSV PCPOSV PDPOSV PZPOSV
полож.определенная экспертный PSPOSVX PCPOSVX PDPOSVX PZPOSVX
симмет./эрмитова простой PSPBSV PCPBSV PDPBSV PZPBSV
полож.определ.ленточная
симмет./эрмитова простой PSPTSV PCPTSV PDPTSV PZPTSV
полож.определ.3 диагон.
Подпрограммы решения линейных задач наименьших квадратов (LLS):
Решение LLS с исп. QR или LQ фактор. PSGELS PCGELS PDGELS PZGELS
Подпрограммы решения задачи на собственные значения и сингулярные значения:
Тип задачи
SEP простой PSSYEV PDSYEV
экспертный PSSYEVX PCHEEVX PDSYEVX PZHEEVX
GSEP экспертный PSSYGVX PCHEGVX PDSYGVX PZHEGVX
SVD PSGESVD PDGESVD
Подпрограммы для вычислительных аспектов с матрицами:
Тип матрицы
общая (частичная факторизац. PSGETRF PCGETRF PDGETRF PZGETRF
перестановка) реш.с исп.ф. PSGETRS PCGETRS PDGETRS PZGETRS
оц.чис.обус. PSGECON PCGECON PDGECON PZGECON
ошибки PSGERFS PCGERFS PDGERFS PZGERFS
обр.с исп.ф. PSGETRI PCGETRI PDGETRI PZGETRI
равновесие PSGEEQU PCGEEQU PDGEEQU PZGEEQU
общая ленточная факторизац. PSGBTRF PCGBTRF PDGBTRF PZGBTRF
(частичная перестановка) реш.с исп.ф. PSGBTRS PCGBTRS PDGBTRS PZGBTRS
общая ленточная факторизац. PSDBTRF PCDBTRF PDDBTRF PZDBTRF
(без перестановки) реш.с исп.ф. PSDBTRS PCDBTRS PDDBTRS PZDBTRS
общая 3 диагональная факторизац. PSDTTRF PCDTTRF PDDTTRF PZDTTRF
(без перестановки)
симмет./эрмитова факторизац. PSPOTRF PCPOTRF PDPOTRF PZPOTRF
полож.определенная реш.с исп.ф. PSPOTRS PCPOTRS PDPOTRS PZPOTRS
оц.чис.обус. PSPOCON PCPOCON PDPOCON PZPOCON
ошибки PSPORFS PCPORFS PDPORFS PZPORFS
обр.с исп.ф. PSPOTRI PCPOTRI PDPOTRI PZPOTRI
равновесие PSPOEQU PCPOEQU PDPOEQU PZPOEQU
симмет./эрмитова факторизац. PSPBTRF PCPBTRF PDPBTRF PZPBTRF
полож.определ.ленточная реш.с исп.ф. PSPBTRS PCPBTRS PDPBTRS PZPBTRS
симмет./эрмитова факторизац. PSPTTRF PCPTTRF PDPTTRF PZPTTRF
полож.определ.3 диагон. реш.с исп.ф. PSPTTRS PCPTTRS PDPTTRS PZPTTRS
треугольная решение PSTRTRS PCTRTRS PDTRTRS PZTRTRS
оц.чис.обус. PSTRCON PCTRCON PDTRCON PZTRCON
ошибки PSTRRFS PCTRRFS PDTRRFS PZTRRFS
обращение PSTRTRI PCTRTRI PDTRTRI PZTRTRI
Подпрограммы вычисления ортогональных разложений:
Тип разложение и матрицы
QR, общая фак.с перест. PSGEQPF PCGEQPF PDGEQPF PZGEQPF
фак.без пер. PSGEQRF PCGEQRF PDGEQRF PZGEQRF
получение Q PSORGQR PCUNGQR PDORGQR PZUNGQR
умнож.на Q PSORMQR PCUNMQR PDORMQR PZUNMQR
LQ, общая фак.без пер. PSGELQF PCGELQF PDGELQF PZGELQF
получение Q PSORGLQ PCUNGLQ PDORGLQ PZUNGLQ
умнож.на Q PSORMLQ PCUNMLQ PDORMLQ PZUNMLQ
QL, общая фак.без пер. PSGEQLF PCGEQLF PDGEQLF PZGEQLF
получение Q PSORGQL PCUNGQL PDORGQL PZUNGQL
умнож.на Q PSORMQL PCUNMQL PDORMQL PZUNMQL
RQ, общая фак.без пер. PSGERQF PCGERQF PDGERQF PZGERQF
получение Q PSORGRQ PCUNGRQ PDORGRQ PZUNGRQ
умнож.на Q PSORMRQ PCUNMRQ PDORMRQ PZUNMRQ
RZ, трапециевидная фак.без пер. PSTZRZF PCTZRZF PDTZRZF PZTZRZF
умнож.на Q PSORMRZ PCUNMRZ PDORMRZ PZUNMRZ
Подпрограммы решения задач с редукцией на собственные значения и сингулярные значения:
Тип матрицы
плот.симм.(или эрмитово) ред.к 3 диаг. PSSYTRD PCHETRD PDSYTRD PZHETRD
ортогон./унитарная (сим. умн.матриц PSORMTR PCUNMTR PDORMTR PZUNMTR
после редук.
пр.PxSYTRD
симметричная 3 диагон. с.з./с.в., QR SSTEQR2 DSTEQR2
симметричная 3 диагон. с.з., бисек. PSSTEBZ PDSTEBZ
с.в.,обр.итер. PSSTEIN PCSTEIN PDSTEIN PZSTEIN
общая ред.Хессенб. PSGEHRD PCGEHRD PDGEHRD PZGEHRD
ортогон./унитарная (нес.) умн.матриц PSORMHR PCUNMHR PDORMHR PZUNMHR
после редук.
Хессенберга
Хессенберговая с.з. и Шура р. PSLAHQR PDLAHQR
симметричная/эрмитово редукция PSSYGST PCHEGST PDSYGST PZHEGST
общая ред.к 2 диаг. PSGEBRD PCGEBRD PDGEBRD PZGEBRD
ортогон./унитарная умн.матриц PSORMBR PCUNMBR PDORMBR PZUNMBR
пос.2 диаг.