IMPROVED FITS TO THE xF3 CCFR DATA
AT THE NEXT-TO-NEXT-TO-LEADING ORDER AND BEYOND
A. L. Kataev
Institute for Nuclear Research of the Academy of Sciences of Russia, Moscow
G. Parente
Department of Particle Physics, University of Santiago de Compostela, Santiago de Compostela, Spain
A. V. Sidorov
Joint Institute for Nuclear Research, Dubna
A review of the analysis of Tevatron data for xF3 structure
function of deep inelastic 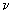 N scattering, provided by CCFR
collaboration, is presented. Special attention is paid
to taking into account of the higher-order perturbative QCD effects
and nonperturbative contributions.
Using the results for
the NNLO QCD corrections to anomalous dimensions
of odd xF3 Mellin moments and N3LO corrections
to their coefficient functions we improve
previous analysis of the CCFR'97 data for xF3.
The possibility of extracting the 1/Q2-corrections from the fits
is analysed using three independent models.
Theoretical question of applicability
of the renormalon-type inspired large- N scattering, provided by CCFR
collaboration, is presented. Special attention is paid
to taking into account of the higher-order perturbative QCD effects
and nonperturbative contributions.
Using the results for
the NNLO QCD corrections to anomalous dimensions
of odd xF3 Mellin moments and N3LO corrections
to their coefficient functions we improve
previous analysis of the CCFR'97 data for xF3.
The possibility of extracting the 1/Q2-corrections from the fits
is analysed using three independent models.
Theoretical question of applicability
of the renormalon-type inspired large-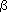 o approximation for
estimating corrections to the coefficient functions of odd xF3
and even nonsinglet F2 moments is considered. The
comparison with [1/1] Pade estimates is given.
The obtained NNLO values of o approximation for
estimating corrections to the coefficient functions of odd xF3
and even nonsinglet F2 moments is considered. The
comparison with [1/1] Pade estimates is given.
The obtained NNLO values of 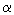 s(MZ) are in agreement with
the world average value s(MZ) are in agreement with
the world average value 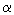 s(MZ) ~ 0.118.
We also present the first
N3LO extraction of s(MZ) ~ 0.118.
We also present the first
N3LO extraction of 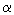 s(MZ).
The interplay between higher-order perturbative QCD
corrections and 1/Q2-terms is demonstrated.
The results of our studies are compared with those
obtained recently using the NNLO model of the kernel of the DGLAP
equation and with the results of the NNLO fits to CCFR'97 xF3 data,
performed by the Bernstein polynomial technique. s(MZ).
The interplay between higher-order perturbative QCD
corrections and 1/Q2-terms is demonstrated.
The results of our studies are compared with those
obtained recently using the NNLO model of the kernel of the DGLAP
equation and with the results of the NNLO fits to CCFR'97 xF3 data,
performed by the Bernstein polynomial technique.
Приведен анализ данных для структурной функции xF3
глубоконеупругого 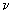 N-рассеяния, полученных на тэватроне коллаборацией CCFR.
Особое внимание уделено учету высших поправок
теории возмущений КХД и вкладам эффектов, возникающих вне рамок
теории возмущений. Используя результаты вычислений трехпетлевых
поправок к аномальным размерностям нечетных моментов Меллина от
xF3 и вкладов более высокого порядка теории возмущений к их
коэффициентным функциям, мы детализируем наши предыдущие работы,
посвященные обработке данных коллаборации CCFR для xF3. В
рамках трех независимых моделей проанализирована возможность
извлечения из фитов поправок порядка 1/Q2. Рассмотрены
теоретические особенности применимости ренормалонного подхода для
оценок высших поправок теории возмущений к коэффициентным функциям
нечетных моментов от xF3 и четных моментов от несинглетной части
структурной функции F2. Проведено сравнение с результатами
применения техники диагональных [1/1] аппроксимантов Падэ.
Полученное в результате фитов трехпетлевое значение константы
связи КХД N-рассеяния, полученных на тэватроне коллаборацией CCFR.
Особое внимание уделено учету высших поправок
теории возмущений КХД и вкладам эффектов, возникающих вне рамок
теории возмущений. Используя результаты вычислений трехпетлевых
поправок к аномальным размерностям нечетных моментов Меллина от
xF3 и вкладов более высокого порядка теории возмущений к их
коэффициентным функциям, мы детализируем наши предыдущие работы,
посвященные обработке данных коллаборации CCFR для xF3. В
рамках трех независимых моделей проанализирована возможность
извлечения из фитов поправок порядка 1/Q2. Рассмотрены
теоретические особенности применимости ренормалонного подхода для
оценок высших поправок теории возмущений к коэффициентным функциям
нечетных моментов от xF3 и четных моментов от несинглетной части
структурной функции F2. Проведено сравнение с результатами
применения техники диагональных [1/1] аппроксимантов Падэ.
Полученное в результате фитов трехпетлевое значение константы
связи КХД 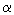 s(MZ) находится в хорошем согласии с ее
среднемировым значением s(MZ) находится в хорошем согласии с ее
среднемировым значением 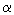 s(MZ)~0,118. Впервые
проведено извлечение значения s(MZ)~0,118. Впервые
проведено извлечение значения 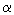 s(MZ) в четырехпетлевом
приближении. Продемонстрирована корреляция между высшими
поправками теории возмущений и вкладами степенных членов,
подавленных 1/Q2. Приведено сравнение результатов нашего
анализа для s(MZ) в четырехпетлевом
приближении. Продемонстрирована корреляция между высшими
поправками теории возмущений и вкладами степенных членов,
подавленных 1/Q2. Приведено сравнение результатов нашего
анализа для 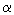 s(MZ) с аналогичными результатами других
работ, в которых использовались приближенное трехпетлевое ядро
уравнения Докшитцера-Грибова-Липатова-Алтарелли-Паризи и метод
полиномов Бернстейна. s(MZ) с аналогичными результатами других
работ, в которых использовались приближенное трехпетлевое ядро
уравнения Докшитцера-Грибова-Липатова-Алтарелли-Паризи и метод
полиномов Бернстейна.
Full text in PDF (478.210)
|
 Home
Home
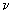 N scattering, provided by CCFR
collaboration, is presented. Special attention is paid
to taking into account of the higher-order perturbative QCD effects
and nonperturbative contributions.
Using the results for
the NNLO QCD corrections to anomalous dimensions
of odd xF3 Mellin moments and N3LO corrections
to their coefficient functions we improve
previous analysis of the CCFR'97 data for xF3.
The possibility of extracting the 1/Q2-corrections from the fits
is analysed using three independent models.
Theoretical question of applicability
of the renormalon-type inspired large-
N scattering, provided by CCFR
collaboration, is presented. Special attention is paid
to taking into account of the higher-order perturbative QCD effects
and nonperturbative contributions.
Using the results for
the NNLO QCD corrections to anomalous dimensions
of odd xF3 Mellin moments and N3LO corrections
to their coefficient functions we improve
previous analysis of the CCFR'97 data for xF3.
The possibility of extracting the 1/Q2-corrections from the fits
is analysed using three independent models.
Theoretical question of applicability
of the renormalon-type inspired large-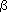 o approximation for
estimating corrections to the coefficient functions of odd xF3
and even nonsinglet F2 moments is considered. The
comparison with [1/1] Pade estimates is given.
The obtained NNLO values of
o approximation for
estimating corrections to the coefficient functions of odd xF3
and even nonsinglet F2 moments is considered. The
comparison with [1/1] Pade estimates is given.
The obtained NNLO values of 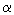 s(MZ) are in agreement with
the world average value
s(MZ) are in agreement with
the world average value