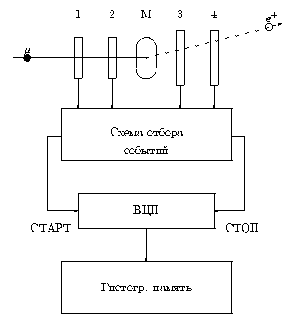
Рис.1.1 Типичная постановка mSR-эксперимента.
| масса (mmu ) | 105.65839(6) MэВ/c2 0.1126 mp = 206.77 me |
| заряд | +e |
| спин (smu) | 1/2 h |
| магнитный момент (mumu ) |
28.0272*10-18 MэВ/Гс 3.18334 mup =0.004836 mue |
| гиромагнитное отношение (gmu /2pi) | 13.55342 кГц/Гс |
| время жизни (tmu ) | 2.19703(4) мкс |
Положительный мюон - элементарная частица класса лептонов, с точки зрения физики конденсированных сред может рассматриваться, как легкий изотоп водорода. Мюоны, имплантированные в вещество, термализуются за время порядка 10-10 секунды, частично сохраняя при этом свою поляризацию, и локализуются в междоузлиях решетки.
Мюон распадается на позитрон, электронное нейтрино и мюонное антинейтрино:
m -> e+ + nue + numu .
Кинетическая энергия позитронов распада изменяется от нуля (импульсы нейтрино и антинейтрино противоположны) до величины
Emax =1/2mmu c2 [1+(me /mmu )2 ]-mec2 ~ 1/2mmuc2 =52.8 MeV, (1.1)
(импульсы нейтрино и антинейтрино совпадают).
Вследствие несохранения четности в слабых взаимодействиях пространственное распределение позитронов от распада мюона будет неизотропно. Вероятность, с которой позитрон испускается в определенном направлении с определенной энергией, в единицу времени дается выражением[21]:
dW(e,y)=1/tmu [1+(2e-1)/(3-2e)Cosy] e2 (3-2e) de dCosy, (1.2)
где e= E/Emax - энергия позитрона в единицах возможной максимальной энергии, y - угол между направлениeм спина мюона в момент распада и импульсом испущенного позитрона, tmu - время жизни мюона.
Коэффициент перед функцией косинуса в (1.2)
называется параметром асимметрии и определяется энергией позитрона. Усреднение по энергии дает Aср = 1/3.
Асимметрия углового распределения позитронов в реакции распада мюона позволяет измерять временную эволюцию поляризации ансамбля мюонов, имплантированных в мишень.
Мюоны получают в реакции распада пионов:
pi-> m + nu
со средним временем жизни пиона tpi = 26 нсек. Пионы, в свою очередь, являются результатом реакций
p + p -> pi + p + n
p + n -> pi + n + n,
которые происходят при взаимодействии протонов, ускоренных до энергии выше порога рождения пионов, с мишенью.
Рассмотрим реакцию получения мюонов в системе отсчета, где пион покоится и будем писать индекс '0' у величин, относящихся к этой системе координат.
При движении по тракту пучка пионы распадаются. Распад пиона является двухчастичной реакцией, поэтому мюон и нейтрино имеют противоположные импульсы. Спин пиона равен нулю, следовательно суммарный спин нейтрино и мюона также равен нулю. Поскольку нейтрино левоспиральная частица, т.е. спин нейтрино всегда противоположен импульсу, то мюон, являющийся продуктом этой реакции, также имеет спин противоположный своему импульсу.
В системе координат покоящегося пиона все направления импульса мюона равновероятны и его энергия равна
Emu0 = c2 (mpi2 + mmu2 )/2mpi = 109.8 MeV (1.3)
В лабораторной системе отсчета мюоны будут равномерно распределены по энергии в интервале от Emin до Emax где
Emax/min = g (Emu0 +/- vpi pmu0
), (1.4)
g = (1-vpi2 /c2 )-1/2 ,
vpi и pmu0 скорость пиона и импульс мюона соответственно.
Возможные направления импульса мюона в лабораторной системе координат образуют конус с углом раствора 2ymax и осью, направленной по скорости пиона, причем
Sin ymax = pmu0 ( g mmu vpi )-1 . (1.5)
Максимальную энергию Emu имеют частицы, чей импульс pmu0 сонаправлен со скоростью пиона vpi и, следовательно, в лабораторной системе координат направление спина противоположно их импульсу. У мюонов с минимальной энергией Emu , чей импульс pmu0 противоположен скорости пиона vpi , в лабораторной системе отсчета спин направлен вдоль импульса. Таким образом, отбирая мюоны по энергии, получают пучок частиц с поляризацией близкой к 100% и направлением спина "по" или "против" импульса частицы.
Гамильтониан взаимодействия в этом случае имеет вид
H = - (mu .B) = - (1/2)gmu h(sB), (1.6)
где mu - магнитный момент мюона, gmu - гиромагнитное отношение
для мюона,
s = (sx ,sy ,sz ),
si - матрицы Паули.
Матрицу плотности для частиц со спином 1/2 можно записать
r = 1/2 .[I + (s.P)], (1.7)
где I - единичная матрица, P - поляризация мюона - вектор, компоненты которого определяются как квантовомеханическое среднее от матриц Паули
Pi = < si >. (1.8)
Подставляя выражения (1.6) и (1.7) в уравнение для матрицы плотности
i h dr/dt = [H(t),r(t)], (1.9)
получим
s dP(t)/dt = i(1/2)gmu [(s B)(s P) - (s P)(s B)]. (1.10)
Учитывая, что
si sj = \deltaij + ieijk sk ,
где eijk - единичный антисимметричный тензор, правую часть (1.10) можно перeписать
si sj (Bi Pj -
Pi Bj ) = (\deltaij +
ieijk sk )(Bi Pj -
Pi Bj ) =
= ieijk (Bi Pj -
Pi Bj ) sk . (1.11)
Поскольку
eijk (Bi Pj -
Pi Bj )
= 2(BxP)k ,
то из (1.10) можно получить выражение для ларморовской прецессии магнитного момента мюона (спина) в магнитном поле
dP(t)/dt = - gmu (BxP). (1.12)
Из (1.12) следует, что компонента поляризации, параллельная полю, сохраняется, а перпендикулярная - прецессирует с частотой
w =gmu |B|. (1.13)
Общее решение уравнения (1.12) имеет вид:
P(t) = A1 + A2 Cos(wt) + A3 Sin(wt), (1.14)
причем A1 , A2 и A3 связаны соотношениями
A1 x n = 0, A2 . n = 0, Axn = A3 ,
где n = B/|B|.
С учетом начального условия
P(0) = P0
решение уравнения (1.12) можно записать
P(t) = (P0 n)n + n x(P0 x n) Cos(wt) + (P0 *n) Sin(wt). (1.15)
Экспериментально определяемой величиной является
поляризация P(t), усредненная по ансамблю частиц - < P(t) >.
Если магнитное поле во всем объеме образца не является строго одинаковым (компоненты поля могут испытывать временные или пространственные флуктуации), то это приведет к тому, что разница в частотах прецессии магнитных моментов вызовет расфазировку прецессии спинов мюонов, локализованных в различных междоузлиях, и модуль поляризации, усредненной по ансамблю частиц, будет изменяться с течением времени.
Для дальнейшего интересен случай, поперечного к направлению начальной поляризации внешнего магнитного поля Bext , когда функция плотности вероятности распределения магнитного поля в образце r(B) имеет следующий вид (1.16)
r(B)=(2pi)-3/2 (DBx DBy DBz)B-1 exp [Bx2/DBx2] exp [By2/DBy2] exp [(Bz -Bz0)2/Bz2] ,
где DBj - дисперсии j-ой компоненты поля, среднее поле направлено по оси z и равно по величине Bz0 . Предположим также, что средняя величина магнитного поля много больше его флуктуаций
Bz0 > > DBx ,DBy ,DBz .
Выражение для поляризации, усредненной по ансамблю частиц, имеет вид интеграла
< P(t) > = Int{ r(B) P(t,B) d3B }. (1.17)
Пусть в начальный момент времени (t=0) поляризация всех мюонов P одинакова по величине и направлена по оси x
P0 = P0 ex ,
тогда для компонент поляризации P(t) из (1.15) можно получить
Px = P0 [bx2 +
(by2 + bz2 ) Cos(wt)], (1.18a)
Py = P0 [bx by -
bx by Cos(wt) - bz Sin(wt)], (1.18b)
Pz = P0 [bx bz - bx bz Cos(wt) + by Sin(wt)], (1.18c)
где bj = Bj / |B|. Подставляя эти выражения в интеграл (1.17) и пренебрегая членами второго порядка малости, находим
< Px > = P0 exp(-(gmu t DBz)2 /2) Cos(gmu Bz t), (1.19a)
< Py > = - P0 exp(-(gmu t DBz)2 /2) Sin(gmu Bz t), (1.19b)
< Pz > = 0. (1.19c)
Таким образом, если отклонения от средней величины магнитного поля малы и распределение поля n(B) гауссово, тогда функция релаксации G(t), определяемая через выражение
|< P(t) >| = |P0| G(t),
имеет вид
G(t) = exp (-\sigma2 t2 /2) (1.20)
где \sigma = gmu DBz - скорость деполяризации.
С помощью положительных мюонов можно изучать и динамические характеристики внутренних магнитных полей в широком диапазоне характерных времен флуктуаций.
Подавляющее большинство mSR экспериментов проводится методом спектроскопии временных интервалов (время-разностной спектроскопии), т.е. измерением интервалов времени между остановкой мюона в веществе и вылетом позитрона распада. Для определения вероятности детектирования позитрона распада dW(e,r) в телесном угле dW с энергией в пределах от e до e+de в единицу времени формулу (1.2) можно переписать в виде
dW(e,er ) = 1/(2\pi tmu ) [1+A(e) P(t)er ] e2 (3-2e) de d\Omega, (1.21)
где er - направление наблюдения, d\Omega = Sin y dy df - телесный угол. Из (1.21) следует, что число зарегистрированных позитронов в направление наблюдения er с энергией e в момент времени t от N0 распадов мюонов, имплантированных в некоторый образец, выражается через
dN(er ,e,t) = (N0 /2\pi tmu ) exp(-t/tmu )
[1 + A(e) < P(t)>er ] e2 (3 - 2e) de d\Omega dt, (1.22)
где < P(t) > - вектор поляризации, усредненный по ансамблю частиц, множитель exp(-t/tmu ) учитывает уменьшение числа мюонов во времени вследствие распада, отсчет времени ведется от момента остановки частицы в образце.
Если эффективность регистрации позитронов не зависит от их энергии, то интегрирование (1.22) по de дает:
dN(r,t)=(N0 /4\pi tmu ) exp(t/tmu ) [1+1/3 < P(t) > er ] d\Omega dt (1.23)
Учет эффективности регистрации позитронов приводит просто к умножению всего выражения на некоторый множитель и замене 1/3 на другой коэффициент.
dN(t)=N0 eff exp(t/tmu ) [1+aeff < P(t) > er ] d\Omega dt (1.24)
Типичная схема постановки mSR-эксперимента приведена на рис.1.1. Пучок поляризованных мюонов вводят в исследуемый образец, где мюоны тормозятся и через некоторое время распадаются. Интенсивность пучка подбирают таким образом, чтобы в каждый момент времени в мишени находился только один мюон, т.к. в противном случае нельзя определить какому мюону сопоставить зарегистрированный позитрон и, поэтому, измерить время между остановкой мюона и вылетом позитрона от его распада.

Остановка поляризованного мюона в исследуемом образце (сигнал "СТАРТ"), определяемая комбинацией сигналов с детекторов 1*2-3 (одновременное срабатывание детекторов 1 и 2 при отсутствии сигнала с детектора 3), запускает время-цифровой преобразователь (ВЦП). Сигнал "СТОП", фиксируемый комбинацией сигналов -1-2*3*4, вырабатывается в момент вылета позитрона распада. Информация об интервалах времени между сигналами "СТАРТ" и "СТОП", т.е. индивидуальное время жизни каждого зарегистрированного мюона, накапливается в памяти многоканального анализатора в виде гистограммы - mSR-спектра.
Обычно mSR-спектр содержит информацию о 106 - 107 событиях m-e распада. Для увеличения объема набираемой статистики может записываться несколько спектров одновременно. Например можно записывать два спектра:
Sf (t) - число обнаруженных позитронов в некотором телесном угле со средним направлением по скорости мюонов в пучке (распады вперед)
Sb (t) - число позитронов в телесном угле со средним направлением обратным первому (распады назад).
Для определения < P(t) > используют полученные гистограммы, описывая их выражением
Si (t) = ki exp(t/tmu ) [1 + di < Pn (t) >] + qi , (1.25)
< Pn (t)> - проекция < P(t) > на некоторое направление, определяемое, взаимным расположением мишени и детекторов. Параметры ki , di , qi учитывают параметры пучка, установки и фоновые события.
Если мюон находится в магнитном поле B, поперечном относительно начальной поляризации, то спин мюона будет прецессировать с частотой w =gmu B, где gmu - гиромагнитное отношение для мюона (см. формулы (1.14) и (1.15)). Это приводит к тому, что вероятность зарегистрировать позитрон от распада мюона становится осциллирующей функцией от времени. Получаемая в этом случае гистограмма описывается выражением
N(t)=N0 exp(-t/tmu )(1+a*P(t)cos(wmu*t+v)) + F (1.26)
где tmu - время жизни мюона, a - наблюдаемая асимметрия m-e распада, P(t) - функция релаксации спина мюона, wmu - частота ларморовской прецессии спина, v - начальная фаза этой прецессии, определяемая, в основном, геометрией установки, F - фон от случайных событий. При измерении локальных магнитных полей в веществе особый интерес представляют wmu и P(t). Ларморовская частота прецессии спина мюона позволяет определить среднюю величину магнитного поля, действующего на мюон. В общем случае таких полей может быть несколько, например, из-за неэквивалентности позиций мюона в кристаллической решетке. Функция релаксации P(t) несет информацию о характере распределения магнитных полей на мюоне. Если деполяризация спина вызвана статическими локальными полями с шириной распределения < B2 >1/2, то функция релаксации приобретает вид P(t)=P0*exp(-\sigma2*t2 ), где \sigma2 =1/2*g2*< B2 > (см. формулу (1.20))
В этой постановке mSR-экспериментов магнитное поле параллельно направлению начальной поляризации спина мюонов. При достаточно большом внешнем магнитном поле (Hext > > Hint ) прецессия спина мюона не наблюдается, но вместо этого появляется возможность изучать динамические характеристики внутренних магнитных полей в веществе. Функция релаксации в этой постановке эксперимента выражается через экспериментальные спектры S и S следующим образом:
Gz (t)=[(Sf(t)- Ff) - Ce(Sb(t)- Fb) ] / [(Sf(t)- Ff) - Ce(Sb(t)+ Fb) ] , (1.27)
где Ff и Fb - фон для переднего и заднего телескопов соответственно, а коэффициент Ce позволяет учитывать разницу в эффективности регистрации позитронов передним и задним телескопами, в том числе из-за различия в телесных углах.
Эксперименты во внешнем продольном магнитном поле Bext > Bint позволяют изучать динамику внутренних магнитных полей Bint . В этом случае функция релаксации спина мюона имеет вид:
Gz (t,Bext,tc )= exp{-(Г*t)1/2 } (1.28)
где tc - характерное время флуктуации (время корреляции) внутреннего магнитного поля. Скорость релаксации Г зависит от tc следующим образом:
Г=\delta tc /(1+wmu2 tc2 ) (1.29)
где \delta - величина, пропорциональная второму моменту распределения внутреннего магнитного поля, wmu =gmu Bext . На рис.1.2 представлены диапазоны характерных времен флуктуаций магнитных полей, измеряемых различными методами.
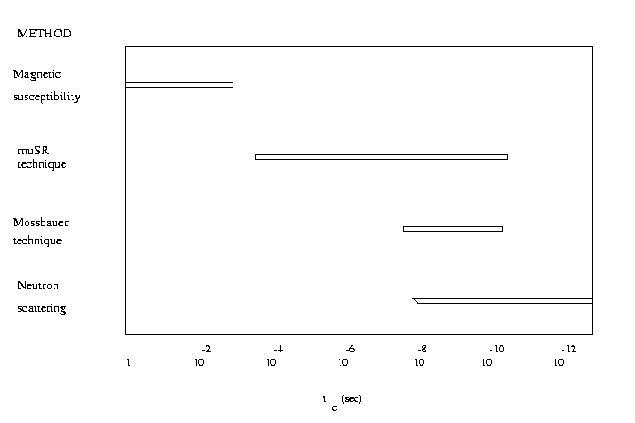
Из рисунка видно, что mSR-метод имеет свое место в ряду других способов изучения динамических флуктуаций внутренних магнитных полей и очень удачно дополняет их.
Эксперименты в поперечном и продольном магнитных полях в предельном случае могут проводиться в нулевом внешнем магнитном поле. Это является большим достоинством mSR-метода, т.к. позволяет исследовать внутренние магнитные поля в веществе без возмущающего воздействия внешнего поля.
В отсутствии внешнего магнитного поля мюон будет прецессировать во внутреннем магнитном поле Hi . Если угол между направлением начальной поляризации спинов мюонов P(0) и Hi равен q, то временная эволюция Pz (t) имеет вид
Pz (t)=cos2 q+sin2 q * cos(gmu Hi t) (1.30)
Это позволяет изучать такие магнитные явления, как магнитоупорядочивание.
Особый интерес представляет случай изотропно распределенных магнитных полей Hi от "замороженных" магнитных моментов - спиновое стекло:
f(Hi,x )=f(Hi,y )=f(Hi,z ) ~ exp(-Hi2 /2*D2 ) (1.31)
Усреднение поляризации по ансамблю на направление детектирования z (1.32) (см.(1.17))
Pz (t)=Int[ f(Hi,x)f(Hi,y)f(Hi,z ) {cos2 q+sin2 q *cos(gmu Hi t)}d3 Hi]
дает
Pz (t)= 1/3 +(2/3)* (1 - gmu2 D2 t2 )* exp(-gmu2 D2 t2/2 ) (1.33)
Эта формула была получена[23] для описания ЯМР сигнала, но наибольшее применение нашла в mSR-исследованиях систем со случайным распределением внутренних магнитных полей.
Из вышесказанного видно, что mSR-метод предоставляет исследователю мощный арсенал средств для всестороннего изучения характеристик внутренних магнитных полей в веществе.
Но метод время-разностной mSR спектроскопии накладывает сильные ограничения на интенсивность пучка мюонов, имплантируемых в образец - для временного анализа отбираются лишь те события m->е распада, когда в течении анализируемого промежутка времени (порядка 10 мкс) в образце останавливается только один мюон и регистрируется один позитрон распада (1m->1е). Это требование ограничивает интенсивность остановок мюонов в образце величиной ; 5*105 m/сек. Это ограничение может быть снято интегральными методами mSR-исследований.
При проведении mSR-экспериментов, требующих высокой точности измерения частоты прецессии спина мюона, а следовательно большой статистики, наилучшие результаты может дать стробоскопический способ измерений, в котором отсутствует ограничение на интенсивность пучка мюонов, связанное с требованием "только 1m и 1e" в фиксированном интервале измерения времен жизни отдельных мюонов. Стробоскопический метод измерения основан на синфазном сложении сигналов позитронов m->e распада от отдельных импульсов (банчей) микроскопической временной структуры мюонного пучка.
Впервые стробоскопический способ измерений был применен для измерения магнитного момента мюона[24], а на импульсном пучке заряженных частиц - в экспериментах по изучению возбужденных гамма-гамма угловых корреляций[25].
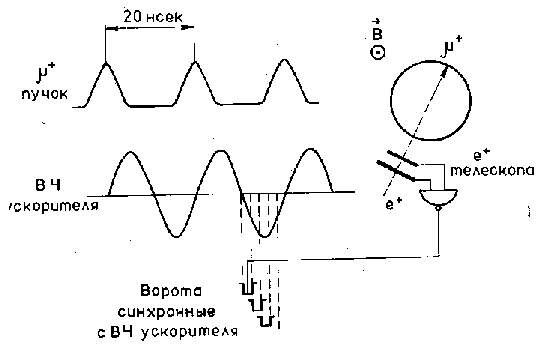
В настоящее время стробоскопический mSR-метод реализован
только на мезонной фабрике PSI (Швейцария) [26](См. рис.1.3).
Временной интервал между импульсами (банчами) мюонного пучка
(20 нс) определяется радиочастотной системой ускорителя
протонов (F=50.633 MГц, DF/F~10-8 ). Поляризованные мюоны,
останавливаясь в образце, прецессируют в магнитном поле B с
ларморовской частотой wmu =gmu*B. Таким
образом, поляризация
мюонов накачивается в образец с частотой повторения F.
Конечная средняя поляризация мюонного ансамбля растет только
в случае, если частота прецессии мюонов совпадает с частотой
повторения импульсов пучка или с одной из ее гармоник m с
точностью, определяемой конечным временем жизни мюона
tm ,
т.e.
Поляризация мюонного ансамбля определяется стробоскопической техникой: позитроны от распада мюонов регистрируются позитронным телескопом, расположенным в плоскости прецессии мюонов во временных воротах, синхронизированных с временной структурой пучка (рис.1.3). Таким образом, позитронный телескоп определяет величину и фазу мюонной поляризации в системе координат, вращающейся с частотой w.
Временные промежутки между соседними импульсами разбиваются на N одинаковых последовательных интервалов ("ворот"), положение которых жестко синхронизировано с положением импульсов. Процедура измерений состоит в определении N суммарных счетов, при регистрации позитронов от распада мюонов во временных "воротах", соответствующих номеру, отсчитываемому от каждого импульса. Таким образом снимаются N зависимостей счетов в воротах Si (H) (i=1...N) от внешнего поля H. Si будет иметь следующий вид:
Si =N0 li (1 + SUM{ Aeff * (2pimF)(cos yi,m - xm sin yi,m)/(1+xm2)} ) , (1.34)
где N0 - общее число позитронов, зарегистрированных позитронным телескопом, li - ширина ворот с номером i, Aeff - эффективная асимметрия, учитывающая конечную ширину банчей мюонного пучка, yi,m - фаза ворот с номером i относительно банчей мюонного пучка. Зависимость количества позитронов, зарегистрированных во временных воротах i, от магнитного поля заключена в величине xm , которая является отклонением частоты прецессии спина мюона от одной из гармоник рабочей частоты ускорителя - xm =(wmu -2pi*m*F)tmu .
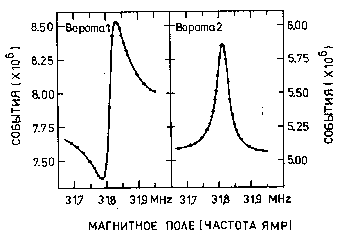
Нетрудно заметить, что при периоде прецессии мюона, кратном интервалу между импульсами, магнитные моменты первоначально поляризованных мюонов будут вращаться синфазно, что приведет, в конечном счете, к резонансным особенностям в зависимостях Si (H). Сравнение этих зависимостей с теоретическими моделями позволяет с высокой точностью определять сдвиг среднего магнитного поля на мюоне в исследуемом образце относительно внешнего поля и оценивать скорость релаксации поляризации мюонов.
На рис.1.4 приведен вид стробоскопического сигнала для двух из десяти стробоскопических ворот. В зависимости от фазы ворот относительно банчей мюонного пучка стробоскопический сигнал имеет форму либо кривой Лоренца, либо дисперсионной кривой, а в общем случае является их суперпозицией.
muSR-спектрометр имеет ряд параметров, характеризующих его, как физический прибор. Отметим некоторые из них.
Временное разрешение в muSR-спектрометрах характеризует способность изучать прецессию спина мюона или мюония на больших частотах. Кроме временных характеристик детекторов во временное разрешение спектрометра входит временное разрешение анализатора, однородность магнитного поля на образце. Величина временного разрешения спектрометра оценивается по уменьшению измеряемого коэффициента асимметрии (амплитуды) прецессии aизм по сравнению с истинной a0 [27]
aизм = а0 exp{ - [\pi2/4*ln2] * [2*tr/T]} (1.35)
где tr - временное разрешение спектрометра, T - период прецессии спина мюона.
Мертвое время (минимальное время регистрации) 2 это временной интервал в начальном участке спектра6 после которого информацию в спектре можно считать достоверной. Факторами, определяющими мертвое время спектрометра являются длительность сигнала антисовпадения, выделяющего остановку мюона, и края кривых совпадений сцинтилляционных телескопов.
Кроме этого важны диапазон температур и магнитных полей, при которых возможно исследование образцов.
Скорость набора информации в muSR спектроскопии временных интервалов ограничена временем жизни мюона, поэтому спектрометры на пучках сравнительно слаботочных ускорителей также успешно используются для проведения mSR исследований.
В Таблице 1.2 приведены основные параметры спектрометров, работающих на пучках мезонных фабрик STUTTGART (PSI, Швейцария)[28], DIZITAL (RAL, Великобритания), OMNI (TRIUMF, Канада)[29] и спектрометра "МЮОНИЙ" (СПИЯФ, Гатчина)[30].
Таблица 1.2.
STUTGART DIZITAL OMNI МЮОНИЙ
Температуры (K) 2,2-300 10-330 4,2-300 4,2-300
Магн. поля (T) 0,3 0,2 0,35 0,05
Разр.время (нс) 1 100 1 1,2
Мертв.время (нс) 10-20 260 10-13 20
После реконструкции фазотрона ОИЯИ встала задача создания mSR-спектрометра и на пучках фазотрона.