Анализ и визуализация данных в физике высоких энергий

Библиотека RooFit предоставляет набор инструментов для моделирования ожидаемого распределения событий в физическом анализе. Модели могут использоваться для выполнения максимально правдоподобного фитирования, создания графиков и применения метода Монте-Карло для различных исследований.

RooFit является расширением ROOT, но по умолчанию не устанавливается вместе с ним. На кластере ЛИТ hybrilit.jinr.ru версия ROOT6 скомпилирована с RooFit. ROOT5 на данном кластере не позволяет пользоваться RooFit.

Основной функциональной возможностью RooFit является возможность моделирования ‘event data’ распределений, где каждое событие - это дискретное событие во времени, и имеет одну или несколько измеряемых наблюдаемых, связанных с ним. Эксперименты такого рода приводят к наборам данных, подчиняющихся статистике Пуассона (или биномиальному распределению).

Язык естественного моделирования для таких распределений - это функция плотности вероятности F(x,р), описывающая плотность вероятности распределения наблюдаемых х как функцию, зависящую от параметра p. В теории вероятностей функция плотности вероятности (P.d.f) или плотность непрерывной случайной величины является функцией, значение которой при любом заданном образце (или точке) в пространстве выборки (набор возможных значений, принимаемых случайной величиной) может быть истолковано как предоставление относительной вероятности того, что значение случайной величины будет равно этой выборке. Определяющие свойства функции плотности вероятностей: нормировка на единицу по всем наблюдаемым и положительная определенность - также дают важные преимущества для проектирования. Функции плотности вероятности легко складываются, возможно построение многомерных P.d.f из одномерных при интуитивно понятном описании корреляций между наблюдаемыми. Также эти функции разрешают универсальное применение метода Монте-Карло.

RooFit использует специальный способ при преобразовании компонентов моделей математических данных в объекты С++; вместо того, чтобы нацеливаться на монолитный объект, который описывает объект данных, каждый математический символ представлен отдельным объектом. Все модели RooFit всегда состоят из нескольких объектов.

Например, функция плотности вероятности Гаусса состоит как правило из четырех объектов: три объекта, представляющие собой наблюдаемую величину, среднее значение и параметр Сигма , и один объект, представляющий функцию плотности вероятности Гаусса. То есть, чтобы иметь возможность работать с функцией плотности вероятности, необходимо создать последовательно все четыре объекта. Аналогичным образом, построение операций, таких как сложение, умножение, интегрирование - представлено отдельными объектамию Такой универсальный язык моделирования хорош для моделей произвольной сложности. Список всех классов библиотеки RooFit с их подробным описанием можно найти по ссылке. RooFit не делает разницы между наблюдаемымы и параметрами. И те, и другие реализуются с помощью класса RooRealVar. Приведем общий вид конструкторов классов RooRealVar и RooGaussian:

RooRealVar::RooRealVar(const char *name, const char *title, Double_t value, Double_t minValue, Double_t maxValue,
const char *unit)

RooGaussian (const char *name, const char *title, RooAbsReal &_x, RooAbsReal &_mean, RooAbsReal &_sigma)
			

Здесь name - имя переменной (сигнала), уникальный идентификатор объекта, title - заголовок переменной (сигнала) с более подробным описанием объекта , value - значение величины, minValue - минимальное значение, maxValue - минимальное значение, unit - единица величины (необязательное значение), x - наблюдаемая величина, mean - среднее значение, sigma - стандартное отклонение.

Объект класса RooAddPdf - эффективная реализация суммы p.d.f в форме

c1 * PDF1 + c2 * PDF2 + ... сп * PDFn или 
c1 * PDF1 + c2 * PDF2 + ... (1-sum (c1 ... сп-1)) * PDFn

Первая форма предназначена для расширенного правдоподобия, где ожидаемое количество событий - Σici. Коэффициенты c_i могут быть либо заданы явно, либо, если все компоненты поддерживают расширенное правдоподобие, они могут быть рассчитаны как вклад каждой p.d.f в общее число ожидаемых событий. Во второй форме сумма коэффициентов принудительно равна единице, а коэффициент последней p.d.f вычисляется из этого условия. Также возможно параметризировать коэффициенты рекурсивно

c1 * PDF1 + (1-с1) (c2 * PDF2 + (1-c2) * (c3 * PDF3 + ....))

В этом виде сумма коэффициентов всегда меньше 1 для всех возможных значений отдельных коэффициентов между 0 и 1. RooAddPdf полагает, что каждый компонент уже нормирован и не выполняет никакой нормировки, кроме вычисления соответствующего последнего коэффициента c_n, если требуется. Условие (принудительное) для этого дополнения состоит в том, что каждый PDF_i не зависит от каждого коэффициента_i.

Рассмотрим пример как построить одномерную функцию плотности вероятности с двумя компонентами: сигналом Гаусса и фоном. Работать с библиотекой RooFit возможно и через интерпретатор CINT и запуская макросы. И в том, и в другом случае рекомендуется в начале обратиться к пространству имен RooFit, чтобы иметь возможность использовать предопределенные константы и другие различные идентификаторы (имена типов, функций, переменных, и т.д.)

root[0] using namespace RooFit;			
root[1] RooRealVar mes("mes","m_{ES} (GeV)",5.20,5.30)      
root[2] RooRealVar sigmean("sigmean","B^{#pm} mass",5.28,5.20,5.30)    
root[3] RooRealVar sigwidth("sigwidth","B^{#pm} width",0.0027,0.001,1.)   
root[4] RooGaussian Signal("Signal","signal PDF",mes,sigmean,sigwidth) 
root[5] RooRealVar argpar("argpar","argus shape parameter",-20.0,-100.,-1.) 
root[6] RooArgusBG background("background","Argus PDF",mes,RooConst(5.291),argpar) 
root[7] RooRealVar nsig("nsig","#signal events",200,0.,10000) 
root[8] RooRealVar nbkg("nbkg","#background events",800,0.,10000) 
root[9] RooAddPdf model("model","g+a",RooArgList(signal,background),RooArgList(nsig,nbkg)) 
root[10] RooDataSet *data = model.generate(mes,2000) 
root[11] model.fitTo(*data) 
root[12] RooPlot* mesframe = mes.frame()
root[13] data->plotOn(mesframe) 
root[14] model.plotOn(mesframe) 
root[15] mesframe->Draw()

Комментарии к примеру:
• [0]-подключаем пространство имен RooFit. (Обратите внимание на необходимость точки с запятой в этой команде).
• [1]-определяем наблюдаемую величину.
• [2-3]-определяем параметры сигнала.
• [4]-конструируем сигнал (в имени переменной используем прописную букву S, чтобы избежать тождественности с именем файла signal.h в стандарте C++ 11.
• [5]-определяем параметры фона.
• [6]-конструируем фон.
• [7-9]-конструируем модель (сигнал+фон).
• [10]-генерируем 2000 событий.
• [11]-выполняем фитирование.
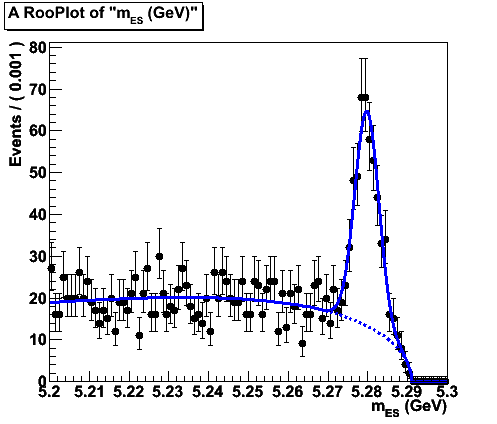
• [12-15]-рисуем комбинированную p.d.f и данные, разыгранные по ней. Объект класса RooPlot - это пустой кадр, способный удерживать что-либо (RooDataSet; проекции PDF и общие проекции вещественных функций; любой ROOT объект: arrows, text boxes, ... - который можно нарисовать) в зависимости от его переменной.

В результате действий, приведенных выше, получим следующую картинку.

Чтобы получить значения mean и sigma используйте метод Print. В данном случае:

root[16] sigmean.Print()
root[17] sigwidth.Print()  

Также можно добавить на экран поле параметров p.d.f и поле статистики:

root[18] model.paramOn(mesframe,data)
root[19] data.statOn(mesframe)
root[20] mesframe->Draw()

Пример свертки двух функций плотности вероятности

В первом примере показано использование оператора сложения двух p.d.f RooAddPdf для составления общей p.d.f. Также возможно построить свертку p.d.f.-ий с использованием оператора свертки, реализованного в классе RooFFTConvPdfF.

root[0] using namespace RooFit ;

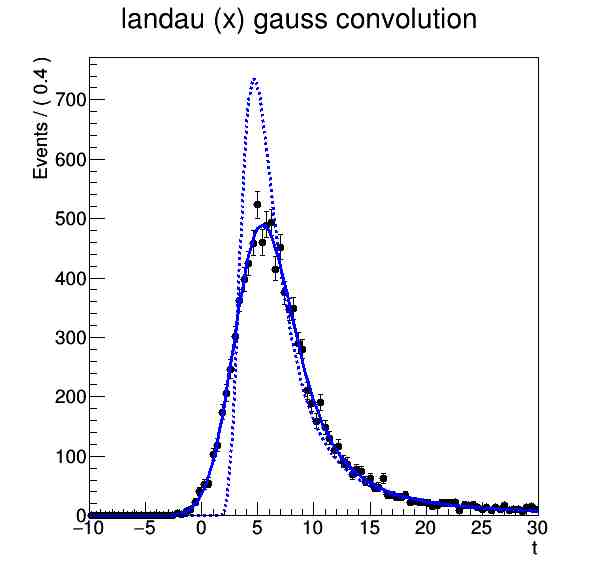
Конструируем наблюдаемую величину t [1], среднее значение и стандартное отклонение для двух распределений Ландау и Гаусса [2-5]. Строим сами распределения [6-7]. Конструируем свертку Ландау и Гаусса . Производим выборку из 10000 событий, фитируем данные Строим график, на котором представлены: функция плотности вероятности получившейся свертки (сплошная линия), данные, разыгранные по этой функции (маркеры) и p.d.f. Ландау (штриховая линия).

root[1] RooRealVar t("t","t",-10,30)
root[2] RooRealVar ml("ml","mean landau",5.,-20,20) 
root[3] RooRealVar sl("sl","sigma landau",1,0.1,10) 
root[4] RooRealVar mg("mg","mean gauss",0) 
root[5] RooRealVar sg("sg","sigma gauss",2,0.1,10) 
root[6] RooLandau landau("lx","lx",t,ml,sl) 
root[7] RooGaussian gauss("gauss","gauss",t,mg,sg) 
  // Set #bins to be used for FFT sampling to 10000
root[8] t.setBins(10000,"cache") ;
root[9] RooFFTConvPdf lxg("lxg","landau (X) gauss",t,landau,gauss) ;
root[10] RooDataSet* data = lxg.generate(t,10000) ;
root[11] lxg.fitTo(*data) ;
root[12] RooPlot* frame = t.frame(Title("landau (x) gauss convolution")) ;
root[13] data->plotOn(frame) ;
root[14] lxg.plotOn(frame) ;
root[15] landau.plotOn(frame,LineStyle(kDashed)) ;
root[16] new TCanvas("convolution","convolution",600,600) ;
root[17] gPad->SetLeftMargin(0.15) ; 
root[18] frame->GetYaxis()->SetTitleOffset(1.4) ; 
root[19] frame->Draw() ;

Пример многомерной p.d.f.

Tакже можно построить многомерную функцию плотности вероятности и ее проекции на оси x и y.

Создаем наблюдаемые:

RooRealVar x("x","x",-5,5) ;
RooRealVar y("y","y",-5,5) ;
   

Создаем параметры и функцию f(y) = a0 + a1*y

   RooRealVar a0("a0","a0",-0.5,-5,5) ;
   RooRealVar a1("a1","a1",-0.5,-1,1) ;
   RooPolyVar fy("fy","fy",y,RooArgSet(a0,a1)) ;

Создаем Гаусс(x,f(y),s)

   RooRealVar sigma("sigma","width of gaussian",0.5) ;
   RooGaussian model("model","Gaussian with shifting mean",x,fy,sigma) ;

Генерируем 10000 событий распределенных по этой модели

  
  RooDataSet *data = model.generate(RooArgSet(x,y),10000) ;

Создаем график x распределения данных и проекцию модели на x = Int(dy) model(x,y)

   RooPlot* xframe = x.frame() ;
   data->plotOn(xframe) ;
   model.plotOn(xframe) ;

Создаем график y распределения данных и проекцию модели на x = Int(dy) model(x,y)

   RooPlot* yframe = y.frame() ;
   data->plotOn(yframe) ;
   model.plotOn(yframe) ;

Создаем двумерную гистограмму x от y

   TH1* hh_model = model.createHistogram("hh_model",x,Binning(50),YVar(y,Binning(50))) ;
   hh_model->SetLineColor(kBlue) ;

Создаем экран и рисуем графики

   TCanvas *c = new TCanvas("rf301_composition","rf301_composition",1200, 400);
   c->Divide(3);
   c->cd(1) ; gPad->SetLeftMargin(0.15) ; xframe->GetYaxis()->SetTitleOffset(1.4) ; xframe->Draw() ;
   c->cd(2) ; gPad->SetLeftMargin(0.15) ; yframe->GetYaxis()->SetTitleOffset(1.4) ; yframe->Draw() ;
   c->cd(3) ; gPad->SetLeftMargin(0.20) ; hh_model->GetZaxis()->SetTitleOffset(2.5) ; hh_model->Draw("surf") ;
   

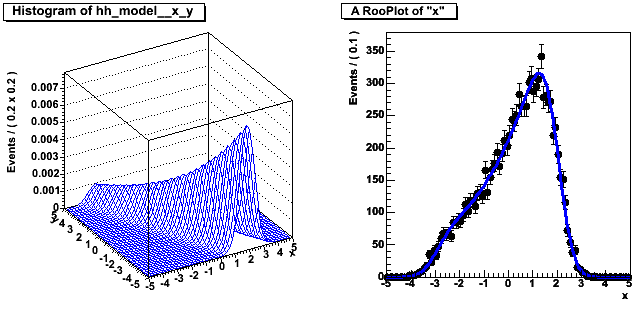
На рисунке снизу приведена двумерная визуализация М(Х,Y) и проекции на наблюдаемыt х и y c наложенными на них данными.

Пример работы с функциями вероятности и их профильными проекциями

В предыдущих примерах проиллюстрированы различные методики для построения функции плотности вероятностей в RooFit. Этот пример демонстрирует различные операции, которые могут быть применены на уровне вероятности. Даны p.d.f и набор данных, функция вероятности может быть построена как

RooAbsReal* nll = pdf.createNLL(data) ;

Функции правдоподобия ведет себя как обычная функция RooFit и может быть построена таким же образом,как функции плотности вероятностей.

RooPlot* frame = myparam.frame() ;
nll->plotOn(frame) ;

Поскольку оценка вероятности являются потенциально трудоемкой операцией, RooFit облегчает расчет вероятности, используя параллельно несколько процессов. Этот процесс распараллеливания является прозрачным для пользователя. Запросив параллельные вычисления на 8 процессорах (на одном узле), можно построить функцию правдоподобия следующим образом

RooAbsReal* nll = pdf.createNLL(data,NumCPU(8)) ;

Можно также по аналогии построить проекции вероятности на разные величины.

RooAbsReal* pll = nll->createProfile(paramOfInterest) 

Рассмотрим пример, как сконструировать p.d.f и набор данных и сравнить вероятность и проекцию вероятности на однин из параметров.

root[1] RooRealVar x("x","x",-20,20) 
root[2] RooRealVar mean("mean","mean of g1 and g2",0,-10,10) 
root[3] RooRealVar sigma_g1("sigma_g1","width of g1",3) 
root[4] RooGaussian g1("g1","g1",x,mean,sigma_g1) 
root[5] RooRealVar sigma_g2("sigma_g2","width of g2",4,3.0,6.0) 
root[6] RooGaussian g2("g2","g2",x,mean,sigma_g2) 
root[7] RooRealVar frac("frac","frac",0.5,0.0,1.0) 
root[8] RooAddPdf model("model","model",RooArgList(g1,g2),frac) // Модель (интенсивные сильные корреляции)
root[9] RooDataSet* data = model.generate(x,1000) 

root[10]   RooAbsReal* nll = model.createNLL(*data,NumCPU(2)) 

root[11] RooMinimizer(*nll).migrad() 

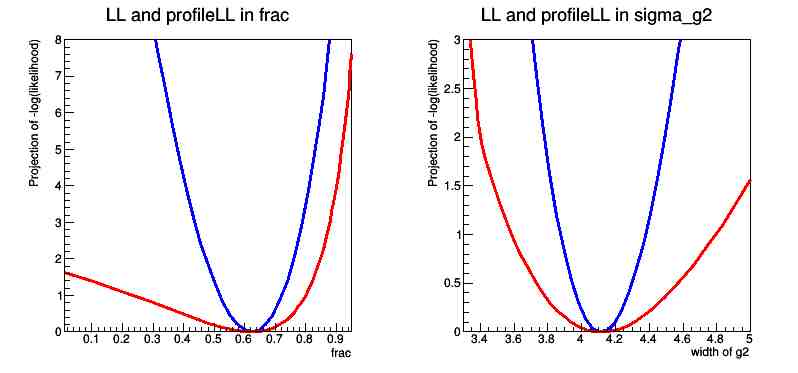
root[12] RooPlot* frame1 = frac.frame(Bins(10),Range(0.01,0.95),Title("LL and profileLL in frac")) 
     root[13] nll->plotOn(frame1,ShiftToZero()) 

root[14] RooPlot* frame2 = sigma_g2.frame(Bins(10),Range(3.3,5.0),Title("LL and profileLL in sigma_g2")) 
     root[15] nll->plotOn(frame2,ShiftToZero()) 

root[16] RooAbsReal* pll_frac = nll->createProfile(frac) 

root[17]   pll_frac->plotOn(frame1,LineColor(kRed)) 

root[18] frame1->SetMinimum(0) 
root[19] frame1->SetMaximum(3) 

root[20] pll_sigmag2->plotOn(frame2,LineColor(kRed)) 

root[21] frame2->SetMinimum(0) 
root[22] frame2->SetMaximum(3) 

root[23] Canvas *c = new TCanvas("rf605_profilell","rf605_profilell",800, 400)
root[24] c->Divide(2)
root[25] c->cd(1) 
root[26] gPad->SetLeftMargin(0.15) 
root[27] frame1->GetYaxis()->SetTitleOffset(1.4)  
root[28] frame1->Draw() 
root[29] c->cd(2)  
root[30] gPad->SetLeftMargin(0.15) 
root[31] frame2->GetYaxis()->SetTitleOffset(1.4)  
root[32] frame2->Draw() 
root[33] delete pll_frac 
root[34] delete pll_sigmag2 
root[35] delete nll 

Получившийся график содержит вероятности и проекцию вероятности на параметр flac, а также аналогичный график для проекции на параметр sigma_g2.

Учебные программы и документация

Набор из 83 учебных макросов (а также ссылка на Руководство пользователя) доступны в дистрибутиве по адресу $ROOTSYS/tutorials/roofit. (На кластере hybrilit - по адресу /cvmfs/hybrilit.jinr.ru/sw/root/6.09.02/sl6-gcc49/tutorials/roofit) Подробная документация всех классов c методами и членами данных доступна на официальном сайте ROOT формате .pdf.