|
|
||||||
|
Theory of Condensed Matter
| Leaders: | V.A. Osipov A.M. Povolotskii |
Participating Countries and International Organizations:
Armenia, Australia, Austria, Belarus, Belgium, Brazil, Bulgaria, Canada, Czech Republic, France, Germany, Hungary, India, Ireland, Italy, Japan, Moldova, Mongolia, Poland, Romania, Russia, Serbia, Slovakia, Slovenia, Spain, Switzerland, Taiwan, Ukraine, USA, Uzbekistan, Vietnam.
Scientific Programme:
Effects of strong electron correlations in high-temperature superconductors, colossal magneto-resistance compounds (manganites), heavy-fermion systems, low-dimensional quantum magnets with strong spin-orbit interaction, topological insulators, etc. will be investigated based on a variety of underlying many-band electronic models including the extended Hubbard model, Anderson model, super-exchange spin-orbital models of transition of metal oxides with strong relativistic spin-orbital coupling. The electronic band structure, spectral properties of charge carrier quasiparticles, magnetic and charge collective excitations, metal-insulator and magnetic phase transitions, Cu- and Fe-based high-Tc superconductivity, charge and spin-orbital ordering will be studied. The obtained results will be used to support neutron scattering experiments performed at FLNP, JINR.
Investigations in the field of nanostructures and nanoscaled phenomena will be addressed to a study of physical characteristics of nanomaterials promising for various applications in modern nanotechnologies. The electronic, thermal and transport properties of carbon nanostructures will be investigated. It is planned to study the problem of quantum transport in molecular devices. Spin dynamics of magnetic nanoclusters will be investigated. The analysis of resonance tunneling phenomena in the layered superconductors and superconducting nanostructures in the external fields will be performed. Numerical modeling of resonance, radiative and chaotic properties of intrinsic Josephson junctions in high temperature superconductors is planned to be carried out.
╠odels in condensed matter physics will be studied by using methods of equilibrium and non-equilibrium statistical mechanics with the aim of revealing general properties of many-particle systems based on the ideas of self-similarity and universality. Mathematical mechanisms, underlying the kinetic and stationary behavior of model systems, as well as possible links between different models, will be investigated. The study of two-dimensional lattice models by the transfer matrix method will be focused on confirming the predictions of the logarithmic conformal field theory. The theory of integrable systems will be developed in the aspect of finding new integrable boundary conditions for two-dimensional spin systems and the solution of the corresponding Yang-Baxter equations. The universal behavior of correlation functions in non-equilibrium systems will be studied as well. The research in the structure theory and the theory of representations of quantum groups and matrix algebras will be directed to further applications in the theory of integrable models in quantum mechanics and statistical physics. Applications of the elliptic hypergeometric integrals, defining the most general solutions of the Yang-Baxter equation and most complicated known exactly computable path integrals in four-dimensional quantum field theory, to two-dimensional spin systems will be studied.
Expected main results in 2017:
- Theoretical study of electronic and magnetic properties of strongly correlated systems including newly synthesized oxides 3d, 4d and 5d transition metals.
Theoretical study of electronic, transport and optical properties of hybrid perovskites for the third generation of solar cells.
Calculation of the spin-wave excitation spectrum, magnetization, susceptibility and the Neel temperature for the quasi-two-dimensional Kitaev-Heisenberg model on the honeycomb lattice proposed for iridates in the antiferromagnetic and paramagnetic states.
Development of the superconducting theory for the quasi-two-dimensional compass- Heisenberg model and the Kitaev-Heisenberg model on the honeycomb lattice.
Investigation of the one-dimensional Bose gas in external potentials. Description of short-range correlations in the Bose gas in the regime of strong interactions.
Development of theoretical models for small-angle scattering from mass and surface fractals. Theoretical study of small-angle scattering from multifractals.
Investigation of generation of magnetic precession by Josephson current in the presence of spin-orbital coupling in the external electromagnetic field.
The classification of the appearing superconducting spintronics effects.
Study of the hopping mechanism of the vibron excitation transport in macromolecular chains in the framework of non-adiabatic polaron theory depending on the quantum state of the macromolecular structural elements, such as squeezed and chaotic squeezed states.
Theoretical investigation of the electron conductivity in polycrystalline graphene. Calculation of a relaxation time due to a finite charged dislocation wall of a different type (grain boundary scattering), and the corresponding contribution to the tensor of conductivity as a function of temperature and carriers concentration.
Application of the extended self-consistent Huckkel method, along with the non-equilibrium Green's function method and finding of the current-voltage characteristics of some graphene nanostructures. Investigation of the influence of the phonon-phonon interaction to the thermal conductance of the graphene nanoribbons with a different width.
Development of the new concepts of electronic nano-devices based on graphene and graphene ribbons. Investigation of different aspects of electron transport in the electronic devices based on the graphene edge states.
Within the dual model of strongly correlated electrons, the spin correlation function is to be computed for the lightly doped cuprates beyond the mean-field approximation.
- Construction of superconformal indices for quiver supersymmetric gauge
theories and description of their relation to partition functions of lattice spin
systems.
Consideration of a traffic model, where a condition of irreversible aggregation is introduced along with the standard conditions of the excluded volume. Irreversible aggregation means that a cluster of particles being emerged once will not be destroyed later and all particles of the cluster move synchronously. The model is defined on a finite interval with a given ingoing and outgoing probabilities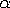 ,
, 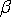 at the ends of interval.
The phase diagram of the stationary state will be constructed and its peculiarities in four different sectors will be explained.
at the ends of interval.
The phase diagram of the stationary state will be constructed and its peculiarities in four different sectors will be explained.
Detailed investigation of the rotor-router aggregation model on infinite graphs.
Investigation of separation of variables in three-body elliptic Calogero-Moser systems.
Computation of large-deviation probabilities in the spherical model, generalized spherical model and in the models of the Boson gas.
Investigation of the structure of quantum matrix algebras of orthogonal and symplectic types, classification of irreducible representations of the braid group B3 in low dimensions.
Solving of spectral problems in systems of mixed dimensionality. Derivation of new characteristics of the equiangular tight frames.
Description of the transition from the Kardar-Parisi-Zhang regime to the deterministic aggregation regime in the non-stationary fluctuations of particle current in the model of generalized asymmetric simple exclusion process. Calculation of the universal finite size corrections to the large deviation function of particle current in the model of random walks in a random environment.
Development of the theory of Bose-condensed systems with dipolar interaction potentials.
Formulation of an approach for describing non-equilibrium networks of complex quantum systems.
Study of the time evolution and stationary states of open many-particle interacting systems by means of a special procedure of a reduced description. The method of maximum information entropy will be analyzed in this context.
Construction of solutions of the Yang-Mills equations on conical spaces with Lorentzian metric in various dimensions. Study of the particle-vortex duality.
| List of Activities | |||
| Activity or experiment | Leaders | ||
| Laboratory or other Division of JINR | Main researchers | ||
| 1. | Complex materials and nanostructures |
V.A. Osipov N.M. Plakida |
|
| BLTP |
| FLNP
|
| LIT
|
| 2. | Contemporary problems of statistical physics | A.M. Povolotsky V.B. Priezzhev |
| BLTP |
| LIT
|
| Collaboration | |||
| Country or International Organization | City | Institute or Laboratory | |
| Armenia | Yerevan | Foundation ANSL | |
| Australia | Melbourne | Univ. | |
| Sydney | Univ. | ||
| Austria | Vienna | TU Wien | |
| Belarus | Minsk | BSTU | |
| IP NASB | |||
| ICE MES RB | |||
| JIPNR-Sosny NASB | |||
| Belgium | Louvain-la-Neuve | UCL | |
| Brazil | Brasilia, DF | UnB | |
| Sao Paulo, SP | USP | ||
| Natal, RN | IIP UFRN | ||
| Bulgaria | Sofia | IMech BAS | |
| ISSP BAS | |||
| SU | |||
| INRNE BAS | |||
| Canada | Montreal | Concordia | |
| Quebec | UL | ||
| Kingston | Queen's | ||
| London | Western | ||
| Czech Republic | Rez | NPI ASCR | |
| France | Annecy-le-Vieux | LAPTh | |
| Paris | UPMC | ||
| Marseille | CPT | ||
| UPC | |||
| Nice | UN | ||
| Valenciennes | UVHC | ||
| Germany | Bonn | UniBonn | |
| Bremen | Univ. | ||
| Braunschweig | TU | ||
| Dortmund | TU Dortmund | ||
| Darmstadt | GSI | ||
| Dresden | IFW | ||
| MPI PkS | |||
| TU Dresden | |||
| Duisburg | UDE | ||
| Leipzig | UoC | ||
| Magdeburg | OVGU | ||
| Rostock | Univ. | ||
| Stuttgart | MPI-FKF | ||
| Wuppertal | UW | ||
| Hungary | Budapest | Wigner RCP | |
| India | Mumbai | TIFR | |
| Ireland | Dublin | DIAS | |
| Italy | Catania | UniCT | |
| Salerno | UNISA | ||
| Japan | Kochi | KUT | |
| Poland | Krakow | JU | |
| Warsaw | IPC PAS | ||
| WUT | |||
| Katowice | US | ||
| Poznan | AMU | ||
| IMP PAS | |||
| Romania | Bucharest | IFIN-HH | |
| Cluj-Napoca | UTC-N | ||
| Timisoara | UVT | ||
| Russia | Moscow | MIREA | |
| NNRU "MEPhI" | |||
| NRU HSE | |||
| PFUR | |||
| SINP MSU | |||
| MI RAS | |||
| NRC KI | |||
| Moscow, Troitsk | HPPI RAS | ||
| Belgorod | BelSU | ||
| Gatchina | PNPI | ||
| Kazan | KFU | ||
| Krasnoyarsk | KIP SB RAS | ||
| Protvino | IHEP | ||
| Saratov | SSU | ||
| St. Petersburg | ETU | ||
| IPTI RAS | |||
| SPbSU | |||
| PDMI RAS | |||
| Voronezh | VSU | ||
| Moldova | Chisinau | IAP ASM | |
| Mongolia | Ulaanbaatar | NUM | |
| Serbia | Belgrade | INS "VINCA" | |
| Slovakia | Bratislava | CU | |
| Kosice | IEP SAS | ||
| TUKE | |||
| Slovenia | Ljubljana | UL | |
| Spain | Madrid | ICMM-CSIC | |
| Switzerland | Villigen | PSI | |
| Zurich | ETH | ||
| Taiwan | Taipei | IP AS | |
| Ukraine | Kharkov | KFTI | |
| Kiev | IMP NASU | ||
| NUK | |||
| L'viv | ICMP NASU | ||
| USA | Louisville, KY | UofL | |
| New York, NY | CUNY | ||
| Rochester, NY | UR | ||
| Tallahassee, FL | FSU | ||
| Uzbekistan | Tashkent | Assoc."P.-S." PTI | |
| Vietnam | Hanoi | IMS VAST |