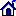Language: Fortran
The subroutine SCATTERH6 calculating a phase shift delta
and wave functions Psi of the Schroedinger equations
with boundary conditions:
Psi(x) -> 0 at x -> 0 or x -> - infinity,
Psi(x) -> sin (kx + delta) at x -> + infinity
on a uniform grid by the Bode quadrature formula [1] with a given
order of accuracy (from 2 up to 6) by the step h on a uniform grid.
Structure:
| Type |
- |
SUBROUTINE |
| User Entry Names |
- |
SCATTERH6 |
| Internal Names |
- |
RSTEP, XIVALUE1, PHI0, PHI1, GAUSSJ, MUU |
| External References |
- |
POT, INITIAL - user-supplied subprograms |
Usage:
CALL SCATTERH6(DLAM1,PSI0,QQ,RMIN,RMAX,R,NN,IPOINT,EPS)
The input datas - QQ, RMIN, RMAX, R, NN, IPOINTS, EPS, where:
| QQ |
- |
is given momentum; |
| RMIN, RMAX |
- |
are minimal and maximal values of independent
variable R on a finite interval [RMIN, RMAX]; |
| R(I) |
- |
are nodes of a grid; |
| NN |
- |
is number of subintervals; |
| IPOINT |
- |
is number of nodes of the Bode quadrature formula
(from 2 up to 6); |
| EPS |
- |
is given accuracy of a calculation process. |
Output datas - DLAM1, PSI0, where:
| DLAM1 |
- |
is value of a phase shift delta; |
| PSI0(I) |
- |
are values of a wave function Psi(R(I)). |
| FUNCTION POT(R) |
- |
is compounded by the user for calculation of
the potential function V(x). |
SUBROUTINE INITIAL
(PSI0,DLAM0,QQ,R,IPOINT,N) |
- |
is compounded by the user for calculation of
asymptotic wave functions PSI0(1)...PSI0(IPOINT-1),
initial approximations: of wave functions
PSI0 (IPOINT)... PSI0 (N) and a phase shift DLAM0. |
Method:
Algorithm, on the basis of which the given subroutine was constructed
described in [2-4].
The accuracy of calculation -
up to O (h ^ (2 [(IPOINT+1) /2]).
Sources are submitted.
References:
- M. Abramowitz, I. Stegun, Handbook of mathematical
functions, National Bureau of Standarts, NY, 1964.
- O. Chuluunbaatar, I.V. Puzynin, S.I. Vinitsky, Journal of
Computational Methods in Sciences and Engineering, 2002, v.2, p.37.
- O. Chuluunbaatar, I.V. Puzynin, S.I. Vinitsky,
JINR preprint P11-01-61, Dubna 2001.
- O. Chuluunbaatar, JINR abstract 11-2002-209, Dubna, 2002.