|
FUNINT Библиотека "JINRLIB"  Автор: Ю.Ю.Лобанов Вы
Язык: Фортран
Автор: Ю.Ю.Лобанов Вы
Язык: Фортран  посетитель.
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛЬНЫХ ИНТЕГРАЛОВ
ОТ ВЕЩЕСТВЕННЫХ ФУНКЦИОНАЛОВ
ИНТЕГРАЛЬНО-ЭКСПОНЕНЦИАЛЬНОГО ВИДА
Программа FUNINT предназначена для приближенного вычисления функциональных
(континуальных) интегралов в задачах физики и математики [1]. В ней
реализован подход к функциональным интегралам и методам их вычисления на
основе определения интеграла Лебега в абстрактных метрических пространствах,
развитый в [1].
В отличие от стохастических методов (Монте-Карло), в данной программе
используются детерминированные алгоритмы для вычисления функциональных
интегралов, разработанные в [2]. Это дает возможность получения результатов
с гарантированной, а не вероятностной оценкой погрешности и обеспечивает
более высокую скорость сходимости приближений к точному значению интеграла.
В программе FUNINT осуществляется вычисление функционального интеграла
посетитель.
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛЬНЫХ ИНТЕГРАЛОВ
ОТ ВЕЩЕСТВЕННЫХ ФУНКЦИОНАЛОВ
ИНТЕГРАЛЬНО-ЭКСПОНЕНЦИАЛЬНОГО ВИДА
Программа FUNINT предназначена для приближенного вычисления функциональных
(континуальных) интегралов в задачах физики и математики [1]. В ней
реализован подход к функциональным интегралам и методам их вычисления на
основе определения интеграла Лебега в абстрактных метрических пространствах,
развитый в [1].
В отличие от стохастических методов (Монте-Карло), в данной программе
используются детерминированные алгоритмы для вычисления функциональных
интегралов, разработанные в [2]. Это дает возможность получения результатов
с гарантированной, а не вероятностной оценкой погрешности и обеспечивает
более высокую скорость сходимости приближений к точному значению интеграла.
В программе FUNINT осуществляется вычисление функционального интеграла
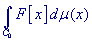 ,
где интегрирование производится по пространству ,
где интегрирование производится по пространству 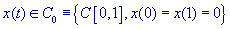 непрерывных на отрезке [0,1] функций с нулевыми значениями на концах отрезка;
непрерывных на отрезке [0,1] функций с нулевыми значениями на концах отрезка;
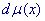 - условная мера Винера на пространстве - условная мера Винера на пространстве 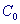 , , 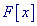 - вещественный
функционал вида - вещественный
функционал вида
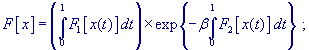
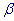 - вещественный параметр, - вещественный параметр, 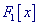 и и 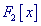 - вещественные функции, задаваемые
пользователем.
Основой для вычисления являются приближенные формулы, описанные в [2].
Данные формулы позволяют находить функциональный интеграл путем вычисления
(n+m) - кратного риманова интеграла, где n и m - произвольные натуральные числа.
Формулы являются точными на классе функциональных многочленов степени - вещественные функции, задаваемые
пользователем.
Основой для вычисления являются приближенные формулы, описанные в [2].
Данные формулы позволяют находить функциональный интеграл путем вычисления
(n+m) - кратного риманова интеграла, где n и m - произвольные натуральные числа.
Формулы являются точными на классе функциональных многочленов степени 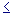 2m+1,
т.е. для функционалов 2m+1,
т.е. для функционалов 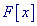 из этого класса остаточный член из этого класса остаточный член 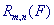 равен нулю.
Для остальных интегрируемых функционалов равен нулю.
Для остальных интегрируемых функционалов 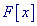 погрешность определяется теоремами,
доказанными в [1]. Как следует из оценки остаточного члена (см. [1]), скорость
сходимости приближений, получаемых по данным формулам к точному значению
интеграла при погрешность определяется теоремами,
доказанными в [1]. Как следует из оценки остаточного члена (см. [1]), скорость
сходимости приближений, получаемых по данным формулам к точному значению
интеграла при  , m фиксировано, имеет порядок , m фиксировано, имеет порядок 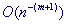 .
В программе FUNINT реализован алгоритм, соответствующий m = 1, т.е. остаточный
член равен нулю для функциональных многочленов степени не выше 3, а в
остальных случаях скорость сходимости имеет порядок .
В программе FUNINT реализован алгоритм, соответствующий m = 1, т.е. остаточный
член равен нулю для функциональных многочленов степени не выше 3, а в
остальных случаях скорость сходимости имеет порядок 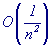 .
Для достижения точности порядка 0.1% обычно бывает достаточно выбрать
значения параметра n порядка 10 или меньше. В программе FUNINT
предусмотрено вычисление n-кратного интеграла по методу Коробова [3]
с использованием библиотечной подпрограммы MIKOR, допускающей значение
кратности k .
Для достижения точности порядка 0.1% обычно бывает достаточно выбрать
значения параметра n порядка 10 или меньше. В программе FUNINT
предусмотрено вычисление n-кратного интеграла по методу Коробова [3]
с использованием библиотечной подпрограммы MIKOR, допускающей значение
кратности k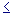 20. Для интегрирования по переменной t в выражении
для 20. Для интегрирования по переменной t в выражении
для 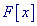 используется библиотечная подпрограмма DSIMPS интегрирования
по Симпсону с двойной точностью.
Литература:
-----------
1. А.Д.Егоров, Е.П.Жидков, Ю.Ю.Лобанов. Введение в теорию и приложения
функционального интегрирования. М: Физматлит, 2006.
2. Yu.Yu.Lobanov. Deterministic computation of functional integrals.
Comp.Phys.Comm., 99 (1996) 59-72.
3. Н.М.Коробов, Теоретико-числовые методы в приближенном анализе.
М.: Физматгиз, 1963.
Структура:
----------
Тип: SUBROUTINE
Имена входа для пользователя: FUNINT
Внутренние подпрограммы: FX, FUNC, FUN1, FUN2, RHO
Внешние подпрограммы: DSIMPS(D120),MIKOR(D121)(из библиотеки JINRLIB)
F1, F2 (составляются пользователем)
Обращение:
----------
CALL FUNINT(K,X,AX,BX,XM,EPS,R), где:
K - суммарная кратность риманова интеграла (K=N+1);
X,AX,BX - рабочие массивы размерности K (должны быть описаны оператором
DIMENSION в основной программе);
XM - значение предела интегрирования по переменной u (может быть
выбрано порядка 4-10 вследствие наличия фактора exp(-u**2)
в зависимости от вида функционала) (см.подробное описание);
EPS - требуемая максимальная относительная погрешность нахождения
функционального интеграла;
R - результат вычисления.
В основной программе перед обращением к FUNINT должны быть также определены
следующие переменные:
B - значение вещественного параметра используется библиотечная подпрограмма DSIMPS интегрирования
по Симпсону с двойной точностью.
Литература:
-----------
1. А.Д.Егоров, Е.П.Жидков, Ю.Ю.Лобанов. Введение в теорию и приложения
функционального интегрирования. М: Физматлит, 2006.
2. Yu.Yu.Lobanov. Deterministic computation of functional integrals.
Comp.Phys.Comm., 99 (1996) 59-72.
3. Н.М.Коробов, Теоретико-числовые методы в приближенном анализе.
М.: Физматгиз, 1963.
Структура:
----------
Тип: SUBROUTINE
Имена входа для пользователя: FUNINT
Внутренние подпрограммы: FX, FUNC, FUN1, FUN2, RHO
Внешние подпрограммы: DSIMPS(D120),MIKOR(D121)(из библиотеки JINRLIB)
F1, F2 (составляются пользователем)
Обращение:
----------
CALL FUNINT(K,X,AX,BX,XM,EPS,R), где:
K - суммарная кратность риманова интеграла (K=N+1);
X,AX,BX - рабочие массивы размерности K (должны быть описаны оператором
DIMENSION в основной программе);
XM - значение предела интегрирования по переменной u (может быть
выбрано порядка 4-10 вследствие наличия фактора exp(-u**2)
в зависимости от вида функционала) (см.подробное описание);
EPS - требуемая максимальная относительная погрешность нахождения
функционального интеграла;
R - результат вычисления.
В основной программе перед обращением к FUNINT должны быть также определены
следующие переменные:
B - значение вещественного параметра 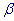 в выражении для функционала в выражении для функционала 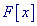 ;
M=1 - значение параметра m;
DX - массив размерности 2 (должен быть описаны оператором DIMENSION):
DX(1) и DX(2) - соответственно начальное и максимальное конечное число
точек многомерной сетки интегрирования для подпрограммы MIKOR;
L - порядок периодизации для подпрограммы MIKOR, 0 ;
M=1 - значение параметра m;
DX - массив размерности 2 (должен быть описаны оператором DIMENSION):
DX(1) и DX(2) - соответственно начальное и максимальное конечное число
точек многомерной сетки интегрирования для подпрограммы MIKOR;
L - порядок периодизации для подпрограммы MIKOR, 0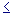 L L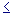 10
(рекомендованные значения L=1,2,3);
H - относительная ширина пограничного слоя для подпрограммы MIKOR
(рекомендуется 0.1 10
(рекомендованные значения L=1,2,3);
H - относительная ширина пограничного слоя для подпрограммы MIKOR
(рекомендуется 0.1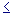 H H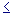 10.0).
Данные переменные должны быть занесены в COMMON-блок PAR:
COMMON/PAR/B,DX(2),L,M,H
Если задать DX(1),DX(2),L,M,H 10.0).
Данные переменные должны быть занесены в COMMON-блок PAR:
COMMON/PAR/B,DX(2),L,M,H
Если задать DX(1),DX(2),L,M,H 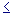 0, то выбор этих величин будет осуществлен
в программе автоматически.
Пользователем должны быть также написаны подпрограммы-функции FUNCTION F1(X)
и FUNCTION F2(X) в соответствии с видом интегрируемого функционала 0, то выбор этих величин будет осуществлен
в программе автоматически.
Пользователем должны быть также написаны подпрограммы-функции FUNCTION F1(X)
и FUNCTION F2(X) в соответствии с видом интегрируемого функционала 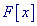 .
Примечания:
-----------
1. При необходимости вычисления функционального интеграла по пространству .
Примечания:
-----------
1. При необходимости вычисления функционального интеграла по пространству
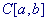 со значениями со значениями 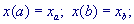 , он может быть преобразован к
интегралу по пространству , он может быть преобразован к
интегралу по пространству 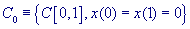 с помощью замены
переменных, описанной в [1].
2. Точность результата и эффективность вычислений во многом зависит от выбора
параметров интегрирования для подпрограммы MIKOR. В случае неудачного
выбора этих параметров и невозможности достижения требуемой точности
выдается соответствующая диагностика.
Архив программы с подробным описанием и исходными текстами.
Работа выполнена в Лаборатории информационных технологий ОИЯИ. с помощью замены
переменных, описанной в [1].
2. Точность результата и эффективность вычислений во многом зависит от выбора
параметров интегрирования для подпрограммы MIKOR. В случае неудачного
выбора этих параметров и невозможности достижения требуемой точности
выдается соответствующая диагностика.
Архив программы с подробным описанием и исходными текстами.
Работа выполнена в Лаборатории информационных технологий ОИЯИ.
|
 Автор: Ю.Ю.Лобанов Вы
Язык: Фортран
Автор: Ю.Ю.Лобанов Вы
Язык: Фортран  посетитель.
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛЬНЫХ ИНТЕГРАЛОВ
ОТ ВЕЩЕСТВЕННЫХ ФУНКЦИОНАЛОВ
ИНТЕГРАЛЬНО-ЭКСПОНЕНЦИАЛЬНОГО ВИДА
Программа FUNINT предназначена для приближенного вычисления функциональных
(континуальных) интегралов в задачах физики и математики [1]. В ней
реализован подход к функциональным интегралам и методам их вычисления на
основе определения интеграла Лебега в абстрактных метрических пространствах,
развитый в [1].
В отличие от стохастических методов (Монте-Карло), в данной программе
используются детерминированные алгоритмы для вычисления функциональных
интегралов, разработанные в [2]. Это дает возможность получения результатов
с гарантированной, а не вероятностной оценкой погрешности и обеспечивает
более высокую скорость сходимости приближений к точному значению интеграла.
В программе FUNINT осуществляется вычисление функционального интеграла
посетитель.
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛЬНЫХ ИНТЕГРАЛОВ
ОТ ВЕЩЕСТВЕННЫХ ФУНКЦИОНАЛОВ
ИНТЕГРАЛЬНО-ЭКСПОНЕНЦИАЛЬНОГО ВИДА
Программа FUNINT предназначена для приближенного вычисления функциональных
(континуальных) интегралов в задачах физики и математики [1]. В ней
реализован подход к функциональным интегралам и методам их вычисления на
основе определения интеграла Лебега в абстрактных метрических пространствах,
развитый в [1].
В отличие от стохастических методов (Монте-Карло), в данной программе
используются детерминированные алгоритмы для вычисления функциональных
интегралов, разработанные в [2]. Это дает возможность получения результатов
с гарантированной, а не вероятностной оценкой погрешности и обеспечивает
более высокую скорость сходимости приближений к точному значению интеграла.
В программе FUNINT осуществляется вычисление функционального интеграла
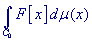 ,
где интегрирование производится по пространству
,
где интегрирование производится по пространству 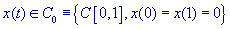 непрерывных на отрезке [0,1] функций с нулевыми значениями на концах отрезка;
непрерывных на отрезке [0,1] функций с нулевыми значениями на концах отрезка;
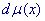 - условная мера Винера на пространстве
- условная мера Винера на пространстве 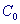 ,
, 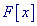 - вещественный
функционал вида
- вещественный
функционал вида
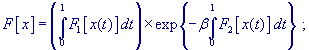
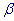 - вещественный параметр,
- вещественный параметр, 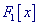 и
и 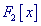 - вещественные функции, задаваемые
пользователем.
Основой для вычисления являются приближенные формулы, описанные в [2].
Данные формулы позволяют находить функциональный интеграл путем вычисления
(n+m) - кратного риманова интеграла, где n и m - произвольные натуральные числа.
Формулы являются точными на классе функциональных многочленов степени
- вещественные функции, задаваемые
пользователем.
Основой для вычисления являются приближенные формулы, описанные в [2].
Данные формулы позволяют находить функциональный интеграл путем вычисления
(n+m) - кратного риманова интеграла, где n и m - произвольные натуральные числа.
Формулы являются точными на классе функциональных многочленов степени 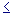 2m+1,
т.е. для функционалов
2m+1,
т.е. для функционалов 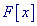 из этого класса остаточный член
из этого класса остаточный член 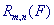 равен нулю.
Для остальных интегрируемых функционалов
равен нулю.
Для остальных интегрируемых функционалов 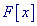 погрешность определяется теоремами,
доказанными в [1]. Как следует из оценки остаточного члена (см. [1]), скорость
сходимости приближений, получаемых по данным формулам к точному значению
интеграла при
погрешность определяется теоремами,
доказанными в [1]. Как следует из оценки остаточного члена (см. [1]), скорость
сходимости приближений, получаемых по данным формулам к точному значению
интеграла при  , m фиксировано, имеет порядок
, m фиксировано, имеет порядок 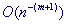 .
В программе FUNINT реализован алгоритм, соответствующий m = 1, т.е. остаточный
член равен нулю для функциональных многочленов степени не выше 3, а в
остальных случаях скорость сходимости имеет порядок
.
В программе FUNINT реализован алгоритм, соответствующий m = 1, т.е. остаточный
член равен нулю для функциональных многочленов степени не выше 3, а в
остальных случаях скорость сходимости имеет порядок 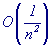 .
Для достижения точности порядка 0.1% обычно бывает достаточно выбрать
значения параметра n порядка 10 или меньше. В программе FUNINT
предусмотрено вычисление n-кратного интеграла по методу Коробова [3]
с использованием библиотечной подпрограммы MIKOR, допускающей значение
кратности k
.
Для достижения точности порядка 0.1% обычно бывает достаточно выбрать
значения параметра n порядка 10 или меньше. В программе FUNINT
предусмотрено вычисление n-кратного интеграла по методу Коробова [3]
с использованием библиотечной подпрограммы MIKOR, допускающей значение
кратности k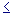 20. Для интегрирования по переменной t в выражении
для
20. Для интегрирования по переменной t в выражении
для 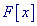 используется библиотечная подпрограмма DSIMPS интегрирования
по Симпсону с двойной точностью.
Литература:
-----------
1. А.Д.Егоров, Е.П.Жидков, Ю.Ю.Лобанов. Введение в теорию и приложения
функционального интегрирования. М: Физматлит, 2006.
2. Yu.Yu.Lobanov. Deterministic computation of functional integrals.
Comp.Phys.Comm., 99 (1996) 59-72.
3. Н.М.Коробов, Теоретико-числовые методы в приближенном анализе.
М.: Физматгиз, 1963.
Структура:
----------
Тип: SUBROUTINE
Имена входа для пользователя: FUNINT
Внутренние подпрограммы: FX, FUNC, FUN1, FUN2, RHO
Внешние подпрограммы: DSIMPS(D120),MIKOR(D121)(из библиотеки JINRLIB)
F1, F2 (составляются пользователем)
Обращение:
----------
CALL FUNINT(K,X,AX,BX,XM,EPS,R), где:
K - суммарная кратность риманова интеграла (K=N+1);
X,AX,BX - рабочие массивы размерности K (должны быть описаны оператором
DIMENSION в основной программе);
XM - значение предела интегрирования по переменной u (может быть
выбрано порядка 4-10 вследствие наличия фактора exp(-u**2)
в зависимости от вида функционала) (см.подробное описание);
EPS - требуемая максимальная относительная погрешность нахождения
функционального интеграла;
R - результат вычисления.
В основной программе перед обращением к FUNINT должны быть также определены
следующие переменные:
B - значение вещественного параметра
используется библиотечная подпрограмма DSIMPS интегрирования
по Симпсону с двойной точностью.
Литература:
-----------
1. А.Д.Егоров, Е.П.Жидков, Ю.Ю.Лобанов. Введение в теорию и приложения
функционального интегрирования. М: Физматлит, 2006.
2. Yu.Yu.Lobanov. Deterministic computation of functional integrals.
Comp.Phys.Comm., 99 (1996) 59-72.
3. Н.М.Коробов, Теоретико-числовые методы в приближенном анализе.
М.: Физматгиз, 1963.
Структура:
----------
Тип: SUBROUTINE
Имена входа для пользователя: FUNINT
Внутренние подпрограммы: FX, FUNC, FUN1, FUN2, RHO
Внешние подпрограммы: DSIMPS(D120),MIKOR(D121)(из библиотеки JINRLIB)
F1, F2 (составляются пользователем)
Обращение:
----------
CALL FUNINT(K,X,AX,BX,XM,EPS,R), где:
K - суммарная кратность риманова интеграла (K=N+1);
X,AX,BX - рабочие массивы размерности K (должны быть описаны оператором
DIMENSION в основной программе);
XM - значение предела интегрирования по переменной u (может быть
выбрано порядка 4-10 вследствие наличия фактора exp(-u**2)
в зависимости от вида функционала) (см.подробное описание);
EPS - требуемая максимальная относительная погрешность нахождения
функционального интеграла;
R - результат вычисления.
В основной программе перед обращением к FUNINT должны быть также определены
следующие переменные:
B - значение вещественного параметра 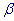 в выражении для функционала
в выражении для функционала 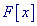 ;
M=1 - значение параметра m;
DX - массив размерности 2 (должен быть описаны оператором DIMENSION):
DX(1) и DX(2) - соответственно начальное и максимальное конечное число
точек многомерной сетки интегрирования для подпрограммы MIKOR;
L - порядок периодизации для подпрограммы MIKOR, 0
;
M=1 - значение параметра m;
DX - массив размерности 2 (должен быть описаны оператором DIMENSION):
DX(1) и DX(2) - соответственно начальное и максимальное конечное число
точек многомерной сетки интегрирования для подпрограммы MIKOR;
L - порядок периодизации для подпрограммы MIKOR, 0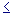 L
L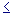 10
(рекомендованные значения L=1,2,3);
H - относительная ширина пограничного слоя для подпрограммы MIKOR
(рекомендуется 0.1
10
(рекомендованные значения L=1,2,3);
H - относительная ширина пограничного слоя для подпрограммы MIKOR
(рекомендуется 0.1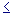 H
H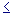 10.0).
Данные переменные должны быть занесены в COMMON-блок PAR:
COMMON/PAR/B,DX(2),L,M,H
Если задать DX(1),DX(2),L,M,H
10.0).
Данные переменные должны быть занесены в COMMON-блок PAR:
COMMON/PAR/B,DX(2),L,M,H
Если задать DX(1),DX(2),L,M,H 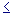 0, то выбор этих величин будет осуществлен
в программе автоматически.
Пользователем должны быть также написаны подпрограммы-функции FUNCTION F1(X)
и FUNCTION F2(X) в соответствии с видом интегрируемого функционала
0, то выбор этих величин будет осуществлен
в программе автоматически.
Пользователем должны быть также написаны подпрограммы-функции FUNCTION F1(X)
и FUNCTION F2(X) в соответствии с видом интегрируемого функционала 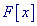 .
Примечания:
-----------
1. При необходимости вычисления функционального интеграла по пространству
.
Примечания:
-----------
1. При необходимости вычисления функционального интеграла по пространству
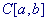 со значениями
со значениями 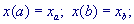 , он может быть преобразован к
интегралу по пространству
, он может быть преобразован к
интегралу по пространству 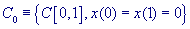 с помощью замены
переменных, описанной в [1].
2. Точность результата и эффективность вычислений во многом зависит от выбора
параметров интегрирования для подпрограммы MIKOR. В случае неудачного
выбора этих параметров и невозможности достижения требуемой точности
выдается соответствующая диагностика.
Архив программы с подробным описанием и исходными текстами.
Работа выполнена в Лаборатории информационных технологий ОИЯИ.
с помощью замены
переменных, описанной в [1].
2. Точность результата и эффективность вычислений во многом зависит от выбора
параметров интегрирования для подпрограммы MIKOR. В случае неудачного
выбора этих параметров и невозможности достижения требуемой точности
выдается соответствующая диагностика.
Архив программы с подробным описанием и исходными текстами.
Работа выполнена в Лаборатории информационных технологий ОИЯИ.



