|
SLIPM Библиотека "JINRLIB"  Авторы: И.В.Пузынин, Т.П.Пузынина, В.Ч.Тхак Вы
Среда программирования: MAPLE/Windows
Авторы: И.В.Пузынин, Т.П.Пузынина, В.Ч.Тхак Вы
Среда программирования: MAPLE/Windows  посетитель.
ПРОГРАММНЫЙ КОМПЛЕКС НА ЯЗЫКЕ MAPLE ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЧАСТИЧНОЙ ПРОБЛЕМЫ
ШТУРМА-ЛИУВИЛЛЯ НА ОСНОВЕ НЕПРЕРЫВНОГО АНАЛОГА МЕТОДА НЬЮТОНА
SLIPM (The Sturm-LIouville Problem in Maple) - программный комплекс на языке
системы компьютерной алгебры MAPLE, состоящий из главной программы SLIPM.mw и
ряда процедур и предназначенный для численного решения с помощью непрерывного
аналога метода Ньютона (НАМН) [1,2] частичной проблемы Штурма-Лиувилля, то есть
для вычисления некоторого собственного значения линейного дифференциального
оператора второго порядка и соответствующей собственной функции, удовлетворяющей
однородным граничным условиям общего вида.
SLIPM является развитием написанных на языке Фортран комплексов программ
SLIP1 [3] и SLIPH4 [4]. Он дополнен двумя новыми способами вычисления начального
значения итерационного параметра
посетитель.
ПРОГРАММНЫЙ КОМПЛЕКС НА ЯЗЫКЕ MAPLE ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЧАСТИЧНОЙ ПРОБЛЕМЫ
ШТУРМА-ЛИУВИЛЛЯ НА ОСНОВЕ НЕПРЕРЫВНОГО АНАЛОГА МЕТОДА НЬЮТОНА
SLIPM (The Sturm-LIouville Problem in Maple) - программный комплекс на языке
системы компьютерной алгебры MAPLE, состоящий из главной программы SLIPM.mw и
ряда процедур и предназначенный для численного решения с помощью непрерывного
аналога метода Ньютона (НАМН) [1,2] частичной проблемы Штурма-Лиувилля, то есть
для вычисления некоторого собственного значения линейного дифференциального
оператора второго порядка и соответствующей собственной функции, удовлетворяющей
однородным граничным условиям общего вида.
SLIPM является развитием написанных на языке Фортран комплексов программ
SLIP1 [3] и SLIPH4 [4]. Он дополнен двумя новыми способами вычисления начального
значения итерационного параметра 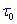 , процедурой уточнения решения (собственного
значения и соответствующей собственной функции) с использованием процедуры
экстраполяции по методу Ричардсона, процедурами графической визуализации
промежуточных и окончательных результатов итерационного процесса, процедурой
сохранения результатов на дисковом файле.
В работах [5,6] дано описание математической постановки исследуемой задачи и
метода ее решения (НАМН). Описаны используемые итерационные ньютоновские
схемы, алгоритмы вычисления начального приближения к решению и итерационного
параметра , процедурой уточнения решения (собственного
значения и соответствующей собственной функции) с использованием процедуры
экстраполяции по методу Ричардсона, процедурами графической визуализации
промежуточных и окончательных результатов итерационного процесса, процедурой
сохранения результатов на дисковом файле.
В работах [5,6] дано описание математической постановки исследуемой задачи и
метода ее решения (НАМН). Описаны используемые итерационные ньютоновские
схемы, алгоритмы вычисления начального приближения к решению и итерационного
параметра 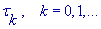 . Даны примеры использования комплекса для вычисления
решений уравнений Шредингера с потенциалом Морзе для мезомолекулы . Даны примеры использования комплекса для вычисления
решений уравнений Шредингера с потенциалом Морзе для мезомолекулы  ,
уравнений Лежандра, Уиттекера.
В работе [7] дано описание процедур программного комплекса и их параметров,
исследован вопрос об оценке точности порядка ,
уравнений Лежандра, Уиттекера.
В работе [7] дано описание процедур программного комплекса и их параметров,
исследован вопрос об оценке точности порядка 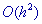 реализованных разностных
схем, описан процесс повышения точности результатов до порядка реализованных разностных
схем, описан процесс повышения точности результатов до порядка  с помощью
процедуры RICHARD, реализующей экстраполяционный метод Ричардсона на
последовательности трех вдвое сгущающихся сеток.
В архиве представлены текст программного комплекса SLIPM_MORSE.mw,
входные данные RICHARDSON1.txt, RICHARDSON2.txt, RICHARDSON4.txt и
выходные файлы SLIPM.txt, SLIPMOH4.txt с результатами.
В предлагаемом здесь тесте приведен пример вычисления безузлового
решения уравнения Шредингера с потенциалом Морзе для мезомолекулы с помощью
процедуры RICHARD, реализующей экстраполяционный метод Ричардсона на
последовательности трех вдвое сгущающихся сеток.
В архиве представлены текст программного комплекса SLIPM_MORSE.mw,
входные данные RICHARDSON1.txt, RICHARDSON2.txt, RICHARDSON4.txt и
выходные файлы SLIPM.txt, SLIPMOH4.txt с результатами.
В предлагаемом здесь тесте приведен пример вычисления безузлового
решения уравнения Шредингера с потенциалом Морзе для мезомолекулы 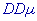 .
Имеются также два набора пользовательских процедур
SLIPM_USER SUPPLIED PROCEDURES_LegendreEquation.mw и
SLIPM_USER SUPPLIED PROCEDURES_WhittakerEquation.mw
для решения уравнений Лежандра и Уиттекера соответственно.
Литература:
-----------
1. И.В. Пузынин и др. Обобщенный непрерывный аналог метода Ньютона для численного
исследования некоторых квантово-полевых моделей. ЭЧАЯ, 1999, Т.30, Вып.1,
с.210-265.
2. И.В. Пузынин и др. О методах вычислительной физики для исследования моделей
сложных физических систем. ЭЧАЯ, 2007, Т.38, Вып.1, с.144-232.
3. I.V. Puzynin, T.P. Puzynina. SLIP1 - Program for the numerical solution of the
Sturm-Liouville problem basing on the continuous analog of the Newton method.
Collection of scientific papers in collaboration of JINR, Dubna, USSR and Central
Research Institute for Physics, Budapest, Hungary, KFKI-74-34, 1974, pp.93-112.
http://www.jinr.ru/programs/jinrlib/slip/
4. I.V. Puzynin, T.P. Puzynina, T.A. Strizh. SLIPH4 - Program for numerical
solution of the Sturm-Liouville problem. JINR Report, P11-87-332, Dubna, 1987.
http://www.jinr.ru/programs/jinrlib/slip/
5. И.В.Пузынин, Т.П. Пузынина, Во Чонг Тхак. SLIPM - программа на языке MAPLE для
численного решения частичной проблемы Штурма-Лиувилля на основе непрерывного
аналога метода Ньютона. Вестник РУДН, серия "Математика. Информатика. Физика"
No.2 вып.2,2010,С.89-97.
6. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
I. Алгоритм. Препринт ОИЯИ Р11-2010-2, Дубна, 2010, С.9.
7. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
II. Программная реализация. Препринт ОИЯИ Р11-2010-95, Дубна, 2010, С.8. .
Имеются также два набора пользовательских процедур
SLIPM_USER SUPPLIED PROCEDURES_LegendreEquation.mw и
SLIPM_USER SUPPLIED PROCEDURES_WhittakerEquation.mw
для решения уравнений Лежандра и Уиттекера соответственно.
Литература:
-----------
1. И.В. Пузынин и др. Обобщенный непрерывный аналог метода Ньютона для численного
исследования некоторых квантово-полевых моделей. ЭЧАЯ, 1999, Т.30, Вып.1,
с.210-265.
2. И.В. Пузынин и др. О методах вычислительной физики для исследования моделей
сложных физических систем. ЭЧАЯ, 2007, Т.38, Вып.1, с.144-232.
3. I.V. Puzynin, T.P. Puzynina. SLIP1 - Program for the numerical solution of the
Sturm-Liouville problem basing on the continuous analog of the Newton method.
Collection of scientific papers in collaboration of JINR, Dubna, USSR and Central
Research Institute for Physics, Budapest, Hungary, KFKI-74-34, 1974, pp.93-112.
http://www.jinr.ru/programs/jinrlib/slip/
4. I.V. Puzynin, T.P. Puzynina, T.A. Strizh. SLIPH4 - Program for numerical
solution of the Sturm-Liouville problem. JINR Report, P11-87-332, Dubna, 1987.
http://www.jinr.ru/programs/jinrlib/slip/
5. И.В.Пузынин, Т.П. Пузынина, Во Чонг Тхак. SLIPM - программа на языке MAPLE для
численного решения частичной проблемы Штурма-Лиувилля на основе непрерывного
аналога метода Ньютона. Вестник РУДН, серия "Математика. Информатика. Физика"
No.2 вып.2,2010,С.89-97.
6. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
I. Алгоритм. Препринт ОИЯИ Р11-2010-2, Дубна, 2010, С.9.
7. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
II. Программная реализация. Препринт ОИЯИ Р11-2010-95, Дубна, 2010, С.8.
|
 Авторы: И.В.Пузынин, Т.П.Пузынина, В.Ч.Тхак Вы
Среда программирования: MAPLE/Windows
Авторы: И.В.Пузынин, Т.П.Пузынина, В.Ч.Тхак Вы
Среда программирования: MAPLE/Windows 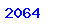 посетитель.
ПРОГРАММНЫЙ КОМПЛЕКС НА ЯЗЫКЕ MAPLE ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЧАСТИЧНОЙ ПРОБЛЕМЫ
ШТУРМА-ЛИУВИЛЛЯ НА ОСНОВЕ НЕПРЕРЫВНОГО АНАЛОГА МЕТОДА НЬЮТОНА
SLIPM (The Sturm-LIouville Problem in Maple) - программный комплекс на языке
системы компьютерной алгебры MAPLE, состоящий из главной программы SLIPM.mw и
ряда процедур и предназначенный для численного решения с помощью непрерывного
аналога метода Ньютона (НАМН) [1,2] частичной проблемы Штурма-Лиувилля, то есть
для вычисления некоторого собственного значения линейного дифференциального
оператора второго порядка и соответствующей собственной функции, удовлетворяющей
однородным граничным условиям общего вида.
SLIPM является развитием написанных на языке Фортран комплексов программ
SLIP1 [3] и SLIPH4 [4]. Он дополнен двумя новыми способами вычисления начального
значения итерационного параметра
посетитель.
ПРОГРАММНЫЙ КОМПЛЕКС НА ЯЗЫКЕ MAPLE ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЧАСТИЧНОЙ ПРОБЛЕМЫ
ШТУРМА-ЛИУВИЛЛЯ НА ОСНОВЕ НЕПРЕРЫВНОГО АНАЛОГА МЕТОДА НЬЮТОНА
SLIPM (The Sturm-LIouville Problem in Maple) - программный комплекс на языке
системы компьютерной алгебры MAPLE, состоящий из главной программы SLIPM.mw и
ряда процедур и предназначенный для численного решения с помощью непрерывного
аналога метода Ньютона (НАМН) [1,2] частичной проблемы Штурма-Лиувилля, то есть
для вычисления некоторого собственного значения линейного дифференциального
оператора второго порядка и соответствующей собственной функции, удовлетворяющей
однородным граничным условиям общего вида.
SLIPM является развитием написанных на языке Фортран комплексов программ
SLIP1 [3] и SLIPH4 [4]. Он дополнен двумя новыми способами вычисления начального
значения итерационного параметра 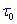 , процедурой уточнения решения (собственного
значения и соответствующей собственной функции) с использованием процедуры
экстраполяции по методу Ричардсона, процедурами графической визуализации
промежуточных и окончательных результатов итерационного процесса, процедурой
сохранения результатов на дисковом файле.
В работах [5,6] дано описание математической постановки исследуемой задачи и
метода ее решения (НАМН). Описаны используемые итерационные ньютоновские
схемы, алгоритмы вычисления начального приближения к решению и итерационного
параметра
, процедурой уточнения решения (собственного
значения и соответствующей собственной функции) с использованием процедуры
экстраполяции по методу Ричардсона, процедурами графической визуализации
промежуточных и окончательных результатов итерационного процесса, процедурой
сохранения результатов на дисковом файле.
В работах [5,6] дано описание математической постановки исследуемой задачи и
метода ее решения (НАМН). Описаны используемые итерационные ньютоновские
схемы, алгоритмы вычисления начального приближения к решению и итерационного
параметра 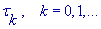 . Даны примеры использования комплекса для вычисления
решений уравнений Шредингера с потенциалом Морзе для мезомолекулы
. Даны примеры использования комплекса для вычисления
решений уравнений Шредингера с потенциалом Морзе для мезомолекулы  ,
уравнений Лежандра, Уиттекера.
В работе [7] дано описание процедур программного комплекса и их параметров,
исследован вопрос об оценке точности порядка
,
уравнений Лежандра, Уиттекера.
В работе [7] дано описание процедур программного комплекса и их параметров,
исследован вопрос об оценке точности порядка 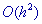 реализованных разностных
схем, описан процесс повышения точности результатов до порядка
реализованных разностных
схем, описан процесс повышения точности результатов до порядка  с помощью
процедуры RICHARD, реализующей экстраполяционный метод Ричардсона на
последовательности трех вдвое сгущающихся сеток.
В архиве представлены текст программного комплекса SLIPM_MORSE.mw,
входные данные RICHARDSON1.txt, RICHARDSON2.txt, RICHARDSON4.txt и
выходные файлы SLIPM.txt, SLIPMOH4.txt с результатами.
В предлагаемом здесь тесте приведен пример вычисления безузлового
решения уравнения Шредингера с потенциалом Морзе для мезомолекулы
с помощью
процедуры RICHARD, реализующей экстраполяционный метод Ричардсона на
последовательности трех вдвое сгущающихся сеток.
В архиве представлены текст программного комплекса SLIPM_MORSE.mw,
входные данные RICHARDSON1.txt, RICHARDSON2.txt, RICHARDSON4.txt и
выходные файлы SLIPM.txt, SLIPMOH4.txt с результатами.
В предлагаемом здесь тесте приведен пример вычисления безузлового
решения уравнения Шредингера с потенциалом Морзе для мезомолекулы 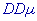 .
Имеются также два набора пользовательских процедур
SLIPM_USER SUPPLIED PROCEDURES_LegendreEquation.mw и
SLIPM_USER SUPPLIED PROCEDURES_WhittakerEquation.mw
для решения уравнений Лежандра и Уиттекера соответственно.
Литература:
-----------
1. И.В. Пузынин и др. Обобщенный непрерывный аналог метода Ньютона для численного
исследования некоторых квантово-полевых моделей. ЭЧАЯ, 1999, Т.30, Вып.1,
с.210-265.
2. И.В. Пузынин и др. О методах вычислительной физики для исследования моделей
сложных физических систем. ЭЧАЯ, 2007, Т.38, Вып.1, с.144-232.
3. I.V. Puzynin, T.P. Puzynina. SLIP1 - Program for the numerical solution of the
Sturm-Liouville problem basing on the continuous analog of the Newton method.
Collection of scientific papers in collaboration of JINR, Dubna, USSR and Central
Research Institute for Physics, Budapest, Hungary, KFKI-74-34, 1974, pp.93-112.
http://www.jinr.ru/programs/jinrlib/slip/
4. I.V. Puzynin, T.P. Puzynina, T.A. Strizh. SLIPH4 - Program for numerical
solution of the Sturm-Liouville problem. JINR Report, P11-87-332, Dubna, 1987.
http://www.jinr.ru/programs/jinrlib/slip/
5. И.В.Пузынин, Т.П. Пузынина, Во Чонг Тхак. SLIPM - программа на языке MAPLE для
численного решения частичной проблемы Штурма-Лиувилля на основе непрерывного
аналога метода Ньютона. Вестник РУДН, серия "Математика. Информатика. Физика"
No.2 вып.2,2010,С.89-97.
6. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
I. Алгоритм. Препринт ОИЯИ Р11-2010-2, Дубна, 2010, С.9.
7. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
II. Программная реализация. Препринт ОИЯИ Р11-2010-95, Дубна, 2010, С.8.
.
Имеются также два набора пользовательских процедур
SLIPM_USER SUPPLIED PROCEDURES_LegendreEquation.mw и
SLIPM_USER SUPPLIED PROCEDURES_WhittakerEquation.mw
для решения уравнений Лежандра и Уиттекера соответственно.
Литература:
-----------
1. И.В. Пузынин и др. Обобщенный непрерывный аналог метода Ньютона для численного
исследования некоторых квантово-полевых моделей. ЭЧАЯ, 1999, Т.30, Вып.1,
с.210-265.
2. И.В. Пузынин и др. О методах вычислительной физики для исследования моделей
сложных физических систем. ЭЧАЯ, 2007, Т.38, Вып.1, с.144-232.
3. I.V. Puzynin, T.P. Puzynina. SLIP1 - Program for the numerical solution of the
Sturm-Liouville problem basing on the continuous analog of the Newton method.
Collection of scientific papers in collaboration of JINR, Dubna, USSR and Central
Research Institute for Physics, Budapest, Hungary, KFKI-74-34, 1974, pp.93-112.
http://www.jinr.ru/programs/jinrlib/slip/
4. I.V. Puzynin, T.P. Puzynina, T.A. Strizh. SLIPH4 - Program for numerical
solution of the Sturm-Liouville problem. JINR Report, P11-87-332, Dubna, 1987.
http://www.jinr.ru/programs/jinrlib/slip/
5. И.В.Пузынин, Т.П. Пузынина, Во Чонг Тхак. SLIPM - программа на языке MAPLE для
численного решения частичной проблемы Штурма-Лиувилля на основе непрерывного
аналога метода Ньютона. Вестник РУДН, серия "Математика. Информатика. Физика"
No.2 вып.2,2010,С.89-97.
6. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
I. Алгоритм. Препринт ОИЯИ Р11-2010-2, Дубна, 2010, С.9.
7. SLIPM - программа на языке MAPLE для численного решения частичной проблемы
Штурма-Лиувилля на основе непрерывного аналога метода Ньютона.
II. Программная реализация. Препринт ОИЯИ Р11-2010-95, Дубна, 2010, С.8.



