Language: Fortran
The FUNINT program is designed to the numerical evaluation of functional
integrals in the problems of physics and mathematics [1]. This program
realizes the approach to the theory of functional integrals and to the
methods of their computations on a basis of definition of the Lebesgue
integral in the abstract metric space, developed in [1].
As distinct from the stochastic methods (Monte-Carlo), this program uses
the deterministic algorithms for computation of functional integrals.
These algorithms have been elaborated in [2]. It gives an opportunity of
obtaining the results with the guaranteed (not probabilistic) error estimate
and ensures the higher speed of convergence of approximations to the exact
value of the integral.
The FUNINT program calculates the following functional integral:
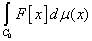 ,
,
where the integration is performed over the space
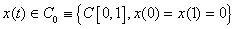
of continuous functions on [0,1] with the zero values at the ends of the
segment;
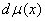
is the conditional Wiener measure on the space
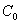
,
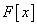
is
the real functional of the form
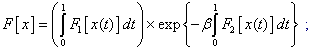
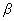
is a real parameter,
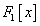
and
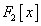
are the real functions that should be
defined by the user.
The basis of computation is formed by the approximation formulas described in [2].
These formulas enable one to evaluate the functional integral by computation
of (n+m) - dimensional Riemann integral, where n and m are arbitrary integer
numbers.
The formulas are exact on a class of polynomial functionals of
degree 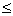 2m+1. It means that for the functionals
2m+1. It means that for the functionals 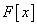 from this class the
remainder term
from this class the
remainder term 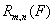 is equal to zero. For all other integrable functionals
is equal to zero. For all other integrable functionals
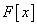 the error of calculation is determined by the theorems proven in [1].
As it follows from estimate of the remainder (see. [1]), the speed of
convergence of approximations, obtained using these formulas, to the exact
value of the integral as
the error of calculation is determined by the theorems proven in [1].
As it follows from estimate of the remainder (see. [1]), the speed of
convergence of approximations, obtained using these formulas, to the exact
value of the integral as 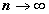 , m fixed, has the order of
, m fixed, has the order of 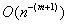 .
.
The FUNINT program uses the algorithm that corresponds to m = 1, i.e. the
remainder term equals zero for the polynomial functionals of degree 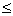 3,
and in all other cases the speed of convergence has the order of
3,
and in all other cases the speed of convergence has the order of 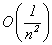 .
.
For the accuracy of about 0.1% it is usually sufficient to choose the value
of parameter n by the order of 10 or smaller. The FUNINT program assumes
computation of n-dimensional integral by the Korobov method [3] using the
existing program MIKOR, which allows using the value of dimension k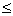 20.
In order to integrate over the variable t in the expression for
20.
In order to integrate over the variable t in the expression for 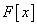 , the
existing program for the double precision integral evaluation by the
Simpson's method, DSIMPS is used.
, the
existing program for the double precision integral evaluation by the
Simpson's method, DSIMPS is used.
References:
- А.Д.Егоров, Е.П.Жидков, Ю.Ю.Лобанов. Введение в теорию и приложения
функционального интегрирования. М: Физматлит, 2006.
- Yu.Yu.Lobanov. Deterministic computation of functional integrals,
Comp. Phys. Comm., 99 (1996) 59-72.
- Н.М.Коробов, Теоретико-числовые методы в приближенном анализе.
М.: Физматгиз, 1963.
Structure:
| Type: |
SUBROUTINE |
| Name: |
FUNINT |
| Internal units: |
FX, FUNC, FUN1, FUN2, RHO |
| External units: |
DSIMPS(D120),MIKOR(D121)(from the program library JINRLIB)
F1, F2 (supplied by the user) |
Usage:
CALL FUNINT(K,X,AX,BX,XM,EPS,R),
Description of the variables:
| K |
- |
total multiplicity of the Riemann integral (K=N+1); |
| X,AX,BX |
- |
working arrays of the length K (must be declared by DIMENSION
statement in the main program); |
| XM |
- |
the value of the upper limit of integration over the variable u
(can be chosen as 4-10 due to existence of the factor
exp(-u**2), depending on the actual form of the functional)
(see detailed description); |
| EPS |
- |
the required relative accuracy of computation of the
functional integral; |
| R |
- |
the result of calculation. |
In the main program before calling FUNINT the following variables must
be defined:
| B |
- |
the value of the real parameter 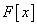 in the expression for the
functional in the expression for the
functional 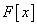 ; ; |
| M=1 |
- |
the value of the parameter m; |
| DX |
- |
array of the length 2 (must be declared by DIMENSION statement): |
| DX(1) и DX(2) |
- |
the initial and the maximal final numbers of points
in the multidimensional integration mesh for the MIKOR program; |
| L |
- |
the periodization order for MIKOR, 0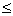 L L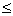 10 (recommended are L=1,2,3); 10 (recommended are L=1,2,3); |
| H |
- |
relative boundary layer width for MIKOR (recommended is 0.1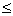 H H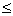 10.0). 10.0). |
These variables must be stored in the COMMON-block PAR:
COMMON/PAR/B,DX(2),L,M,H
If the variables DX(1),DX(2),L,M and H are set 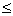 0, the choice of the
values for these variables will be done in the program automatically.
0, the choice of the
values for these variables will be done in the program automatically.
The user must also write the functions FUNCTION F1(X) and FUNCTION F2(X)
in accordance with the form of the integrated functional 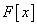 .
.
Remarks:
- If the functional integral over the space
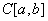 with the boundary
values
with the boundary
values 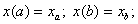 , is to be calculated, it can be transformed
to the integral over the space
, is to be calculated, it can be transformed
to the integral over the space 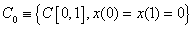 using the change
of the variables described in [1].
using the change
of the variables described in [1].
- The accuracy of the result and the efficiency of calculations depend
on the choice of the integration parameters using by MIKOR.
In case of improper definition of these parameters and when the required
accuracy cannot be reached, the corresponding diagnostic will be displayed.
Detailed description and sources (in Russian) are submitted.
The investigation has been performed at the Laboratory of Information
Technologies, JINR.
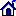



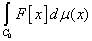 ,
,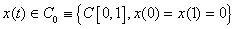 of continuous functions on [0,1] with the zero values at the ends of the
segment;
of continuous functions on [0,1] with the zero values at the ends of the
segment;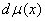 is the conditional Wiener measure on the space
is the conditional Wiener measure on the space 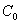 ,
,  is
the real functional of the form
is
the real functional of the form 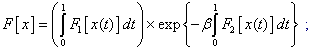
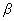 is a real parameter,
is a real parameter, 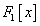 and
and 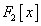 are the real functions that should be
defined by the user.
are the real functions that should be
defined by the user.
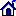




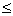 2m+1. It means that for the functionals
2m+1. It means that for the functionals 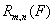 is equal to zero. For all other integrable functionals
is equal to zero. For all other integrable functionals
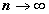 , m fixed, has the order of
, m fixed, has the order of 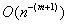 .
.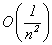 .
.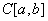 with the boundary
values
with the boundary
values 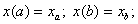 , is to be calculated, it can be transformed
to the integral over the space
, is to be calculated, it can be transformed
to the integral over the space 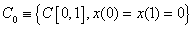 using the change
of the variables described in [1].
using the change
of the variables described in [1].