Languages: Maple, Fortran
The program is designed to construct d-dimensional p-ordered quadrature rules in expanded form for integration over the d-dimensional standard unit simplex Δd
with the vertices 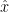 j
= (
j
= (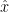 j1
,...,
j1
,..., 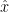 jd
),
jd
), 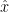 jk
= δjk
, j=0,...d, k=1,...d,
jk
= δjk
, j=0,...d, k=1,...d,
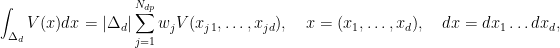
where
|Δd| = 1/d! is the volume of the simplex. Here
Ndp is the number of nodes,
wj are the weights, and
(xj1,...,xjd) are the nodes.
A detailed description of the method for constructing fully symmetric quadrature rules with positive weights, and with points lying inside the 2-,...,6- simplex (so-called PI-type) is published in [1].
The *.mw and *.f files contain the Maple and Fortran programs for converting quadrature formulas up to the 20-th order on a triangle and a tetrahedron, the 16-th order on a 4-simplex, the 10-th order on 5- and 6- simplexes in expanded form, and examples of their application:
- • on INPUT:
- ○ `ddxoy_z.dat' file,
- • on OUTPUT:
- ○ wg is an array of weights with a dimension of gnodes,
- ○ xg is an array of barycentric coordinates of nodes with a dimension of (dim+1)*gnodes.
The `ddxoy_z.dat' files contain the dimension of the simplex, the order of the quadrature rule, the number of nodes, the information about orbits, and PI-type fully symmetric quadrature rules in barycentric coordinates
(y1,...,yd+1) in compact form, where
- • x=dim means the dimension of the simplex,
- • y=p means the order of the quadrature rule,
- • z=gnodes means the number of nodes.
As an example, we consider the integral
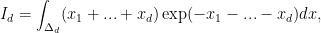
The integral
Id is calculated analytically and for
d=2,...,6 is equal to:
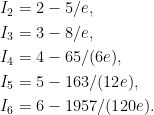
Note that the obtained barycentric coordinates
(yj1,...,yjd+1) of nodes can be used for integration over the
d-dimensional arbitrary simplex
Δq
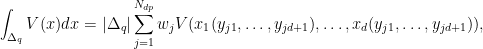
where the volume of the simplex
|Δq| must be calculated separately.
Download the INQSIM program archive.
References:
- G. Chuluunbaatar, O. Chuluunbaatar, A.A. Gusev, and S.I. Vinitsky.
PI-type fully symmetric quadrature rules on the 3-,...,6-simplexes.
Computers & Mathematics with Applications, 124, 89--97 (2022).
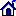



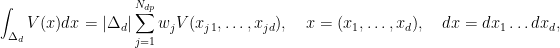
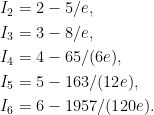




 j
= (
j
= (