|
|
|

|
PROGRAM LIBRARY JINRLIBRK4-MPI - parallel implementation of the numerical solution of the Cauchy problem |
|
|
|
|
Language: C++ The RK4-MPI program is designed for parallel numerical solution of the Cauchy problem in the form 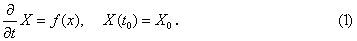 Here X is a vector-column of unknowns consisting of sequentially arranged L blocks of length M. The function f is such that for each i-th equation of the system it depends only on elements of the vector X with numbers i, i+1, and i-1. Similar problems often arise when approximating partial dif-ferential equations using finite difference formulas. This structure of the right side function f in (1) allows you to organize a parallel implementation of the Runge - Kutta calculation based on the dis-tribution of M-length blocks between parallel MPI-processes so that exchange occurs only between the processes with neighboring numbers. Such a scheme of parallel implementation of the Runge-Kutta method was used, for example, in [1] for numerical study of superconducting processes in a system of long Josephson junctions, as well as in [2] for computer simulation of the passage of a multicomponent gas-condensate mixture through a porous medium. Calculations show a 5-10 time reduction in the execution time when running in parallel mode (depending on the dimension of the task and on the number of parallel processes involved) compared to a sequential calculation on a single node. The program RK4-MPI calculates the one step of integration of the system (1) using the fourth or-der Runge-Kutta formula [3]. In the RK4 function, each MPI-process involved calculates, with a given initial value t=t0 and a given initial state X=X0, the values of elements of array X in the segment assigned to it for t=t0+ht. The ff function is called from RK4 to organize the interprocessor exchange of the boundary data. The call of the RK4 function has the form: Input parameters:
♦ f - a user-defined function to calculate the right side of the system (1);
♦ g - a user-defined function for assembling the process-distributed segments of the array X into a single process with the number 0 and storing the results at the current value of the variable t; ♦ M - the size of each of the L consecutive blocks in the array X (the total length of the array of un-knowns is L*M); ♦ t and ht - the initial value of the variable t and the integration step in t (the size of the integration step is determined by the features of a particular problem, including when solving discrete analogues of partial differential equations, the corresponding Courant condition must be taken into account); ♦ m0 - the number of the first M-element block in the segment assigned to each process in the global block numbering; ♦ m1, m2 - the numbers of the first and last block of the array X in each process; ♦ X - a fragment of the total array of unknowns, consisting in each process of sequentially arranged blocks of length M with numbers from m1 to m2 and containing the input values X0 of the corre-sponding elements ;X ♦ Y - a fragment of the array of unknowns, containing in each process the results of integration at t+ht. The array Y can match X. In the functions f (t, m0, m1, m2, * X, * dx) and g(t, m0, m1, m2, * X, * dx), the parameters t, m0, m1, m2, X have the same sense as in the RK4 procedure; dx is an array containing a segment of time derivatives calculated by each process. The user program must include the following lines:
#include "mpi,h"
#include "RK4.cpp" The user program must be designed in accordance with the requirements of the MPI standard. It should call MPI functions that return the number of the MPI process in the group and the total number of processes. For example, like this:
...
int main() {
int argc = 0; char **argv = NULL;
...MPI_Init(&argc, &argv); MPI_Comm_size( comm, &NP ); //NP - number of processes MPI_Comm_rank( comm, &IP); / / IP-number of each process MPI_Finalize(); ... } In addition, the user must organize the calculation of the values m0,m1,m2 before calling the RK4 function, as is done in the example RK4test.cpp (see the section "Markup of MPI processes"). The test example demonstrates the application of the Runge - Kutta numerical method for solving the heat conduction problem on a two-dimensional grid in spatial coordinates, which allows us to demonstrate the distribution of a large amount of calculations between processes. The description of the initial problem statement, the finite-difference system of equations, and the features of using the RK4 function to solve it are presented in the description.pdf file. Files RK4test.cpp, RK4test. par, and RK4test.out contain the code, input data, and calculation results, respectively. The input data in RK4test.par is L and M - the number and size of blocks in the array X, n-the number of integration steps, ht-the integration step. The program archive contains:
1. File RK4.cpp (RK4 and ff functions)
2. Test program RK4test.cpp 3. RK4test.par - file with input parameters 4. RK4test.out - file with the results of the calculation 5. test_description.pdf - description of the test task and the structure of the test program Download the RK4-MPI program archive. References


|
|

