|
OPEM2 Библиотека "JINRLIB"  Автор: Богданова Н.Б.
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) Вы
Язык: Фортран 77
Автор: Богданова Н.Б.
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) Вы
Язык: Фортран 77  Платформа: Windows посетитель.
МЕТОД РАЗЛОЖЕНИЯ ПО ОРТОНОРМИРОВАННЫМ ПОЛИНОМАМ ОТ ДВУХ ПЕРЕМЕННЫХ
И ЕГО РЕАЛИЗАЦИЯ В ВИДЕ ПАКЕТА ПРОГРАММ OPEM2
Пакет программ OPEM2 разрабатывался с 1981 для калибровочных задач
измерительных систем в физике высоких энергий в сотрудничестве с
ЛИТ ОИЯИ, г.Дубна.
Последние версии пакета сделаны при поддержке Болгарского национального
фонда научных исследований по физике - Phi 1001.
1.Описание метода
В OPEM2 используется метод ортогонализации полиномов, основанный на
трехчленном соотношении Хаусхолдера-Форсайта [1,2] (для одномерного
случая) и рекуррентном соотношении Вейсфельда [3] (для многомерного
случая). Семейство полиномов {PL} задается рекуррентным соотношением:
Платформа: Windows посетитель.
МЕТОД РАЗЛОЖЕНИЯ ПО ОРТОНОРМИРОВАННЫМ ПОЛИНОМАМ ОТ ДВУХ ПЕРЕМЕННЫХ
И ЕГО РЕАЛИЗАЦИЯ В ВИДЕ ПАКЕТА ПРОГРАММ OPEM2
Пакет программ OPEM2 разрабатывался с 1981 для калибровочных задач
измерительных систем в физике высоких энергий в сотрудничестве с
ЛИТ ОИЯИ, г.Дубна.
Последние версии пакета сделаны при поддержке Болгарского национального
фонда научных исследований по физике - Phi 1001.
1.Описание метода
В OPEM2 используется метод ортогонализации полиномов, основанный на
трехчленном соотношении Хаусхолдера-Форсайта [1,2] (для одномерного
случая) и рекуррентном соотношении Вейсфельда [3] (для многомерного
случая). Семейство полиномов {PL} задается рекуррентным соотношением:
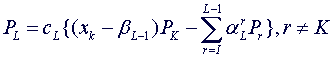 (1.1)
где Pk - базовый полином. K и I вычисляются в процессе работы программы.
{PL} определяются на конечном дискретном подмножестве D пространства (1.1)
где Pk - базовый полином. K и I вычисляются в процессе работы программы.
{PL} определяются на конечном дискретном подмножестве D пространства 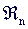 ,
D={q1,q2,...,qM}. Каждая точка qj=qj(x1j1,x2j2,...,xnjn) представляет собой
n-координатный вектор (в данном случае n=2). Веса wj=1/S2j, ассоциированные
с этими точками, зависят от стандартных отклонений в каждой точке.
Точки, веса и значения экспериментальной функции {qj,wj,fjexp}j=1M
в этих точках должны быть заданы. Рекурентные коэффициенты { ,
D={q1,q2,...,qM}. Каждая точка qj=qj(x1j1,x2j2,...,xnjn) представляет собой
n-координатный вектор (в данном случае n=2). Веса wj=1/S2j, ассоциированные
с этими точками, зависят от стандартных отклонений в каждой точке.
Точки, веса и значения экспериментальной функции {qj,wj,fjexp}j=1M
в этих точках должны быть заданы. Рекурентные коэффициенты {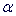 L}, { L}, {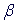 L-1}
и нормализующий фактор {cL} вычисляются как скалярное произведение
от заданных значений. Данное описание есть развитие работ [3,4,7].
В OPEM2 аппроксимируемая функция разлагается по ортонормированным
полиномам с использованием специальных ортонормированных коэффициентов ak.
Оптимальное значение степени полиномов Lr вычисляется, исходя из двух
критериев. L-1}
и нормализующий фактор {cL} вычисляются как скалярное произведение
от заданных значений. Данное описание есть развитие работ [3,4,7].
В OPEM2 аппроксимируемая функция разлагается по ортонормированным
полиномам с использованием специальных ортонормированных коэффициентов ak.
Оптимальное значение степени полиномов Lr вычисляется, исходя из двух
критериев.
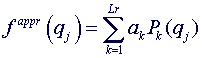 (1.2)
Тогда ортонормированные коэффициенты {ak} в (1.2) легко вычисляются
из заданных значений: (1.2)
Тогда ортонормированные коэффициенты {ak} в (1.2) легко вычисляются
из заданных значений:
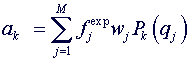 (1.3)
Представим двумерные полиномы в виде пирамиды в порядке возрастания
степени полиномов: (1.3)
Представим двумерные полиномы в виде пирамиды в порядке возрастания
степени полиномов:
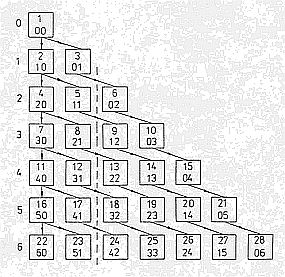 В каждой ячейке пирамиды сверху записан номер полинома, а степени j1 и j2
первого и второго аргумента x1 и x2 приведены ниже.
Пример вычисления индексов K и I в (1.1) для полинома P13 (k=2, j1=2, j2=2):
В каждой ячейке пирамиды сверху записан номер полинома, а степени j1 и j2
первого и второго аргумента x1 и x2 приведены ниже.
Пример вычисления индексов K и I в (1.1) для полинома P13 (k=2, j1=2, j2=2):
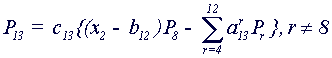 (1.4)
(P8 - базовый полином: K=8, I=4).
В работе [7] для двумерного случая представлены новые теоретические
исследования - для случая дифференцирования и интегрирования в уравнение
(1.1) добавлен четвертый член. Более детальное описание математического
метода для многомерных полиномов, включая дифференцирование и
интегрирование, будет опубликовано позднее в подходящем журнале
в соответствии с настоящим описанием и с некоторыми дополнениями.
2.Описание пакета OPEM2 (Фортран 77)
OPEM2 состоит из главной программы CALIB и пяти подпрограмм:
TSTWO, ORTTWO, PRETWO (основные), DEGREE, NUMBER (вспомогательные).
В главной программе CALIB задаются:
M - количество точек (узлов);
X и Y - массивы координат точек;
F - значения аппроксимируемой функции в узлах;
W - значения весовых коэффициентов.
Основные подпрограммы содержат COMMON-блок /LINKS/, куда записываются
коэффициенты рекуррентного соотношения и вспомогательные переменные.
Размеры массивов в /LINKS/ зависят от суммы индексов j1 и j2, и когда эта
сумма равна 16, размеры массивов определяются как Lmax=(16+1)(16+2)/2=153.
Они могут изменяться в зависимости от задачи.
Подпрограмма TSTWO(X,Y,W,M,F,A,NDEG) организует вызов других подпрограмм.
Сначала TSTWO вызывает PRETWO для подготовки коэффициентов рекуррентных
соотношений с предельной степенью NDEG, подсчитывает ортонормированные
коэффициенты A, вызывая подпрограмму ORTTWO, определяет аппроксимируемые
значения и отклонения в точках, выбирает оптимальную степень Lr и
минимум ( (1.4)
(P8 - базовый полином: K=8, I=4).
В работе [7] для двумерного случая представлены новые теоретические
исследования - для случая дифференцирования и интегрирования в уравнение
(1.1) добавлен четвертый член. Более детальное описание математического
метода для многомерных полиномов, включая дифференцирование и
интегрирование, будет опубликовано позднее в подходящем журнале
в соответствии с настоящим описанием и с некоторыми дополнениями.
2.Описание пакета OPEM2 (Фортран 77)
OPEM2 состоит из главной программы CALIB и пяти подпрограмм:
TSTWO, ORTTWO, PRETWO (основные), DEGREE, NUMBER (вспомогательные).
В главной программе CALIB задаются:
M - количество точек (узлов);
X и Y - массивы координат точек;
F - значения аппроксимируемой функции в узлах;
W - значения весовых коэффициентов.
Основные подпрограммы содержат COMMON-блок /LINKS/, куда записываются
коэффициенты рекуррентного соотношения и вспомогательные переменные.
Размеры массивов в /LINKS/ зависят от суммы индексов j1 и j2, и когда эта
сумма равна 16, размеры массивов определяются как Lmax=(16+1)(16+2)/2=153.
Они могут изменяться в зависимости от задачи.
Подпрограмма TSTWO(X,Y,W,M,F,A,NDEG) организует вызов других подпрограмм.
Сначала TSTWO вызывает PRETWO для подготовки коэффициентов рекуррентных
соотношений с предельной степенью NDEG, подсчитывает ортонормированные
коэффициенты A, вызывая подпрограмму ORTTWO, определяет аппроксимируемые
значения и отклонения в точках, выбирает оптимальную степень Lr и
минимум (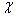 )2, подсчитывает ошибки и печатает результаты.
X и Y - одномерные массивы координат точек (узлов);
W - значения весовых коэффициентов в каждом узле;
M - количество точек;
F - заданная функция;
A - ортонормированные коэффициенты;
NDEG - максимальная предельная степень полиномов.
Подпрограмма ORTTWO(NUMBMX,X,Y,POLY) в POLY-массиве возвращает конкретные
значения полиномов от 1 до NUMBMX при заданных значениях x и y.
NUMBMX - значение Lr - оптимальная степень полиномов;
X и Y - координаты точек, где вычисляются полиномы;
POLY - одномерный массив результатов.
Подпрограмма PRETWO(M,MAXD,X,Y,W,POLY) подготавливает коэффициенты
рекуррентного соотношения двумерных полиномов, ортонормированных на
дискретном точечном множестве.
M - количество точек;
MAXD - максимальная предельная степень, для которой вычисляются
коэффициенты рекуррентного соотношения (как NDEG в TSTWO);
X и Y - одномерные массивы, содержащие координаты точек;
W - значения весовых коэффициентов;
POLY - одномерный массив результатов.
PRETWO делает последовательный рекурсивный вызов подпрограммы ORTTWO,
начиная с NUMBMX = L-1. Следующий вызов ORTTWO выполняется со значением
L, увеличенным на 1, и так далее до тех пор, пока L не достигнет
значения Lmax.
Подпрограмма DEGREE(N,J,JX,JY) считает для данного порядкового номера N
предельную степень его главного члена J, степень x-переменных JX и
степень y-переменных JY.
Функция NUMBER(JX,JY) наоборот, по заданным JX и JY возвращает порядковый
номер полинома в соответствии с [3].
3.Применение
В работах [5,6,7] описаны применения пакета OPEM2 для получения
калибровочных коэффициентов между идеальной и измеренной сетками в
оптических измерительных приборах физики высоких энергий. Последнее
применение пакета - для эксперимента H1 в DESY (Hamburg) - нахождение
координат максимума поверхности, полученной суммированием гауссианов.
Аналитическая поверхность построена на сетке, заданной более чем 400
точками. Работа сделана в коллаборации с ЛИТ ОИЯИ (г.Дубна).
4.Литература
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Архив программы OPEM2 с исходными текстами и результатами. )2, подсчитывает ошибки и печатает результаты.
X и Y - одномерные массивы координат точек (узлов);
W - значения весовых коэффициентов в каждом узле;
M - количество точек;
F - заданная функция;
A - ортонормированные коэффициенты;
NDEG - максимальная предельная степень полиномов.
Подпрограмма ORTTWO(NUMBMX,X,Y,POLY) в POLY-массиве возвращает конкретные
значения полиномов от 1 до NUMBMX при заданных значениях x и y.
NUMBMX - значение Lr - оптимальная степень полиномов;
X и Y - координаты точек, где вычисляются полиномы;
POLY - одномерный массив результатов.
Подпрограмма PRETWO(M,MAXD,X,Y,W,POLY) подготавливает коэффициенты
рекуррентного соотношения двумерных полиномов, ортонормированных на
дискретном точечном множестве.
M - количество точек;
MAXD - максимальная предельная степень, для которой вычисляются
коэффициенты рекуррентного соотношения (как NDEG в TSTWO);
X и Y - одномерные массивы, содержащие координаты точек;
W - значения весовых коэффициентов;
POLY - одномерный массив результатов.
PRETWO делает последовательный рекурсивный вызов подпрограммы ORTTWO,
начиная с NUMBMX = L-1. Следующий вызов ORTTWO выполняется со значением
L, увеличенным на 1, и так далее до тех пор, пока L не достигнет
значения Lmax.
Подпрограмма DEGREE(N,J,JX,JY) считает для данного порядкового номера N
предельную степень его главного члена J, степень x-переменных JX и
степень y-переменных JY.
Функция NUMBER(JX,JY) наоборот, по заданным JX и JY возвращает порядковый
номер полинома в соответствии с [3].
3.Применение
В работах [5,6,7] описаны применения пакета OPEM2 для получения
калибровочных коэффициентов между идеальной и измеренной сетками в
оптических измерительных приборах физики высоких энергий. Последнее
применение пакета - для эксперимента H1 в DESY (Hamburg) - нахождение
координат максимума поверхности, полученной суммированием гауссианов.
Аналитическая поверхность построена на сетке, заданной более чем 400
точками. Работа сделана в коллаборации с ЛИТ ОИЯИ (г.Дубна).
4.Литература
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Архив программы OPEM2 с исходными текстами и результатами.
|
 Автор: Богданова Н.Б.
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) Вы
Язык: Фортран 77
Автор: Богданова Н.Б.
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) Вы
Язык: Фортран 77  Платформа: Windows посетитель.
МЕТОД РАЗЛОЖЕНИЯ ПО ОРТОНОРМИРОВАННЫМ ПОЛИНОМАМ ОТ ДВУХ ПЕРЕМЕННЫХ
И ЕГО РЕАЛИЗАЦИЯ В ВИДЕ ПАКЕТА ПРОГРАММ OPEM2
Пакет программ OPEM2 разрабатывался с 1981 для калибровочных задач
измерительных систем в физике высоких энергий в сотрудничестве с
ЛИТ ОИЯИ, г.Дубна.
Последние версии пакета сделаны при поддержке Болгарского национального
фонда научных исследований по физике - Phi 1001.
1.Описание метода
В OPEM2 используется метод ортогонализации полиномов, основанный на
трехчленном соотношении Хаусхолдера-Форсайта [1,2] (для одномерного
случая) и рекуррентном соотношении Вейсфельда [3] (для многомерного
случая). Семейство полиномов {PL} задается рекуррентным соотношением:
Платформа: Windows посетитель.
МЕТОД РАЗЛОЖЕНИЯ ПО ОРТОНОРМИРОВАННЫМ ПОЛИНОМАМ ОТ ДВУХ ПЕРЕМЕННЫХ
И ЕГО РЕАЛИЗАЦИЯ В ВИДЕ ПАКЕТА ПРОГРАММ OPEM2
Пакет программ OPEM2 разрабатывался с 1981 для калибровочных задач
измерительных систем в физике высоких энергий в сотрудничестве с
ЛИТ ОИЯИ, г.Дубна.
Последние версии пакета сделаны при поддержке Болгарского национального
фонда научных исследований по физике - Phi 1001.
1.Описание метода
В OPEM2 используется метод ортогонализации полиномов, основанный на
трехчленном соотношении Хаусхолдера-Форсайта [1,2] (для одномерного
случая) и рекуррентном соотношении Вейсфельда [3] (для многомерного
случая). Семейство полиномов {PL} задается рекуррентным соотношением:
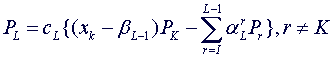 (1.1)
где Pk - базовый полином. K и I вычисляются в процессе работы программы.
{PL} определяются на конечном дискретном подмножестве D пространства
(1.1)
где Pk - базовый полином. K и I вычисляются в процессе работы программы.
{PL} определяются на конечном дискретном подмножестве D пространства 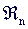 ,
D={q1,q2,...,qM}. Каждая точка qj=qj(x1j1,x2j2,...,xnjn) представляет собой
n-координатный вектор (в данном случае n=2). Веса wj=1/S2j, ассоциированные
с этими точками, зависят от стандартных отклонений в каждой точке.
Точки, веса и значения экспериментальной функции {qj,wj,fjexp}j=1M
в этих точках должны быть заданы. Рекурентные коэффициенты {
,
D={q1,q2,...,qM}. Каждая точка qj=qj(x1j1,x2j2,...,xnjn) представляет собой
n-координатный вектор (в данном случае n=2). Веса wj=1/S2j, ассоциированные
с этими точками, зависят от стандартных отклонений в каждой точке.
Точки, веса и значения экспериментальной функции {qj,wj,fjexp}j=1M
в этих точках должны быть заданы. Рекурентные коэффициенты {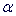 L}, {
L}, {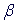 L-1}
и нормализующий фактор {cL} вычисляются как скалярное произведение
от заданных значений. Данное описание есть развитие работ [3,4,7].
В OPEM2 аппроксимируемая функция разлагается по ортонормированным
полиномам с использованием специальных ортонормированных коэффициентов ak.
Оптимальное значение степени полиномов Lr вычисляется, исходя из двух
критериев.
L-1}
и нормализующий фактор {cL} вычисляются как скалярное произведение
от заданных значений. Данное описание есть развитие работ [3,4,7].
В OPEM2 аппроксимируемая функция разлагается по ортонормированным
полиномам с использованием специальных ортонормированных коэффициентов ak.
Оптимальное значение степени полиномов Lr вычисляется, исходя из двух
критериев.
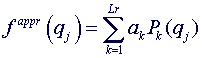 (1.2)
Тогда ортонормированные коэффициенты {ak} в (1.2) легко вычисляются
из заданных значений:
(1.2)
Тогда ортонормированные коэффициенты {ak} в (1.2) легко вычисляются
из заданных значений:
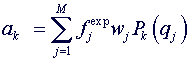 (1.3)
Представим двумерные полиномы в виде пирамиды в порядке возрастания
степени полиномов:
(1.3)
Представим двумерные полиномы в виде пирамиды в порядке возрастания
степени полиномов:
 В каждой ячейке пирамиды сверху записан номер полинома, а степени j1 и j2
первого и второго аргумента x1 и x2 приведены ниже.
Пример вычисления индексов K и I в (1.1) для полинома P13 (k=2, j1=2, j2=2):
В каждой ячейке пирамиды сверху записан номер полинома, а степени j1 и j2
первого и второго аргумента x1 и x2 приведены ниже.
Пример вычисления индексов K и I в (1.1) для полинома P13 (k=2, j1=2, j2=2):
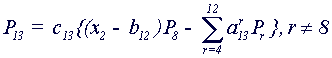 (1.4)
(P8 - базовый полином: K=8, I=4).
В работе [7] для двумерного случая представлены новые теоретические
исследования - для случая дифференцирования и интегрирования в уравнение
(1.1) добавлен четвертый член. Более детальное описание математического
метода для многомерных полиномов, включая дифференцирование и
интегрирование, будет опубликовано позднее в подходящем журнале
в соответствии с настоящим описанием и с некоторыми дополнениями.
2.Описание пакета OPEM2 (Фортран 77)
OPEM2 состоит из главной программы CALIB и пяти подпрограмм:
TSTWO, ORTTWO, PRETWO (основные), DEGREE, NUMBER (вспомогательные).
В главной программе CALIB задаются:
M - количество точек (узлов);
X и Y - массивы координат точек;
F - значения аппроксимируемой функции в узлах;
W - значения весовых коэффициентов.
Основные подпрограммы содержат COMMON-блок /LINKS/, куда записываются
коэффициенты рекуррентного соотношения и вспомогательные переменные.
Размеры массивов в /LINKS/ зависят от суммы индексов j1 и j2, и когда эта
сумма равна 16, размеры массивов определяются как Lmax=(16+1)(16+2)/2=153.
Они могут изменяться в зависимости от задачи.
Подпрограмма TSTWO(X,Y,W,M,F,A,NDEG) организует вызов других подпрограмм.
Сначала TSTWO вызывает PRETWO для подготовки коэффициентов рекуррентных
соотношений с предельной степенью NDEG, подсчитывает ортонормированные
коэффициенты A, вызывая подпрограмму ORTTWO, определяет аппроксимируемые
значения и отклонения в точках, выбирает оптимальную степень Lr и
минимум (
(1.4)
(P8 - базовый полином: K=8, I=4).
В работе [7] для двумерного случая представлены новые теоретические
исследования - для случая дифференцирования и интегрирования в уравнение
(1.1) добавлен четвертый член. Более детальное описание математического
метода для многомерных полиномов, включая дифференцирование и
интегрирование, будет опубликовано позднее в подходящем журнале
в соответствии с настоящим описанием и с некоторыми дополнениями.
2.Описание пакета OPEM2 (Фортран 77)
OPEM2 состоит из главной программы CALIB и пяти подпрограмм:
TSTWO, ORTTWO, PRETWO (основные), DEGREE, NUMBER (вспомогательные).
В главной программе CALIB задаются:
M - количество точек (узлов);
X и Y - массивы координат точек;
F - значения аппроксимируемой функции в узлах;
W - значения весовых коэффициентов.
Основные подпрограммы содержат COMMON-блок /LINKS/, куда записываются
коэффициенты рекуррентного соотношения и вспомогательные переменные.
Размеры массивов в /LINKS/ зависят от суммы индексов j1 и j2, и когда эта
сумма равна 16, размеры массивов определяются как Lmax=(16+1)(16+2)/2=153.
Они могут изменяться в зависимости от задачи.
Подпрограмма TSTWO(X,Y,W,M,F,A,NDEG) организует вызов других подпрограмм.
Сначала TSTWO вызывает PRETWO для подготовки коэффициентов рекуррентных
соотношений с предельной степенью NDEG, подсчитывает ортонормированные
коэффициенты A, вызывая подпрограмму ORTTWO, определяет аппроксимируемые
значения и отклонения в точках, выбирает оптимальную степень Lr и
минимум (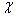 )2, подсчитывает ошибки и печатает результаты.
X и Y - одномерные массивы координат точек (узлов);
W - значения весовых коэффициентов в каждом узле;
M - количество точек;
F - заданная функция;
A - ортонормированные коэффициенты;
NDEG - максимальная предельная степень полиномов.
Подпрограмма ORTTWO(NUMBMX,X,Y,POLY) в POLY-массиве возвращает конкретные
значения полиномов от 1 до NUMBMX при заданных значениях x и y.
NUMBMX - значение Lr - оптимальная степень полиномов;
X и Y - координаты точек, где вычисляются полиномы;
POLY - одномерный массив результатов.
Подпрограмма PRETWO(M,MAXD,X,Y,W,POLY) подготавливает коэффициенты
рекуррентного соотношения двумерных полиномов, ортонормированных на
дискретном точечном множестве.
M - количество точек;
MAXD - максимальная предельная степень, для которой вычисляются
коэффициенты рекуррентного соотношения (как NDEG в TSTWO);
X и Y - одномерные массивы, содержащие координаты точек;
W - значения весовых коэффициентов;
POLY - одномерный массив результатов.
PRETWO делает последовательный рекурсивный вызов подпрограммы ORTTWO,
начиная с NUMBMX = L-1. Следующий вызов ORTTWO выполняется со значением
L, увеличенным на 1, и так далее до тех пор, пока L не достигнет
значения Lmax.
Подпрограмма DEGREE(N,J,JX,JY) считает для данного порядкового номера N
предельную степень его главного члена J, степень x-переменных JX и
степень y-переменных JY.
Функция NUMBER(JX,JY) наоборот, по заданным JX и JY возвращает порядковый
номер полинома в соответствии с [3].
3.Применение
В работах [5,6,7] описаны применения пакета OPEM2 для получения
калибровочных коэффициентов между идеальной и измеренной сетками в
оптических измерительных приборах физики высоких энергий. Последнее
применение пакета - для эксперимента H1 в DESY (Hamburg) - нахождение
координат максимума поверхности, полученной суммированием гауссианов.
Аналитическая поверхность построена на сетке, заданной более чем 400
точками. Работа сделана в коллаборации с ЛИТ ОИЯИ (г.Дубна).
4.Литература
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Архив программы OPEM2 с исходными текстами и результатами.
)2, подсчитывает ошибки и печатает результаты.
X и Y - одномерные массивы координат точек (узлов);
W - значения весовых коэффициентов в каждом узле;
M - количество точек;
F - заданная функция;
A - ортонормированные коэффициенты;
NDEG - максимальная предельная степень полиномов.
Подпрограмма ORTTWO(NUMBMX,X,Y,POLY) в POLY-массиве возвращает конкретные
значения полиномов от 1 до NUMBMX при заданных значениях x и y.
NUMBMX - значение Lr - оптимальная степень полиномов;
X и Y - координаты точек, где вычисляются полиномы;
POLY - одномерный массив результатов.
Подпрограмма PRETWO(M,MAXD,X,Y,W,POLY) подготавливает коэффициенты
рекуррентного соотношения двумерных полиномов, ортонормированных на
дискретном точечном множестве.
M - количество точек;
MAXD - максимальная предельная степень, для которой вычисляются
коэффициенты рекуррентного соотношения (как NDEG в TSTWO);
X и Y - одномерные массивы, содержащие координаты точек;
W - значения весовых коэффициентов;
POLY - одномерный массив результатов.
PRETWO делает последовательный рекурсивный вызов подпрограммы ORTTWO,
начиная с NUMBMX = L-1. Следующий вызов ORTTWO выполняется со значением
L, увеличенным на 1, и так далее до тех пор, пока L не достигнет
значения Lmax.
Подпрограмма DEGREE(N,J,JX,JY) считает для данного порядкового номера N
предельную степень его главного члена J, степень x-переменных JX и
степень y-переменных JY.
Функция NUMBER(JX,JY) наоборот, по заданным JX и JY возвращает порядковый
номер полинома в соответствии с [3].
3.Применение
В работах [5,6,7] описаны применения пакета OPEM2 для получения
калибровочных коэффициентов между идеальной и измеренной сетками в
оптических измерительных приборах физики высоких энергий. Последнее
применение пакета - для эксперимента H1 в DESY (Hamburg) - нахождение
координат максимума поверхности, полученной суммированием гауссианов.
Аналитическая поверхность построена на сетке, заданной более чем 400
точками. Работа сделана в коллаборации с ЛИТ ОИЯИ (г.Дубна).
4.Литература
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Архив программы OPEM2 с исходными текстами и результатами.



