|
OPEM2 Library "JINRLIB"  Author: Nina B.Bogdanova
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) You are
Language: Fortran 77
Author: Nina B.Bogdanova
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) You are
Language: Fortran 77  Platform: Windows visitor here.
ORTHONORMAL POLYNOMIAL EXPANSION METHOD IN TWO DIMENSIONS
AND ITS REALIZATION IN FORTRAN PACKAGE OPEM2
A package of Fortran 77 programs is presented. This package has developed
since 1981 for the calibration problems of measurement devices in High
Energy Physics in collaboration with LIT JINR, Dubna.
Last version of the package is developed in part under the contract
of Bulgarian National Council for Sientific Research - Phi 1001.
1.Description of the Method
Orthonormal Polynomial Expansion Method (OPEM2) is the method of
orthogonalization of polynomials based on Householder-Forsythe
3-term relation [1,2] (one-dimensional case) and the Weisfeld
recurrence [3] (many-dimensional case). The recurrence family of
polynomials {PL} is given by:
Platform: Windows visitor here.
ORTHONORMAL POLYNOMIAL EXPANSION METHOD IN TWO DIMENSIONS
AND ITS REALIZATION IN FORTRAN PACKAGE OPEM2
A package of Fortran 77 programs is presented. This package has developed
since 1981 for the calibration problems of measurement devices in High
Energy Physics in collaboration with LIT JINR, Dubna.
Last version of the package is developed in part under the contract
of Bulgarian National Council for Sientific Research - Phi 1001.
1.Description of the Method
Orthonormal Polynomial Expansion Method (OPEM2) is the method of
orthogonalization of polynomials based on Householder-Forsythe
3-term relation [1,2] (one-dimensional case) and the Weisfeld
recurrence [3] (many-dimensional case). The recurrence family of
polynomials {PL} is given by:
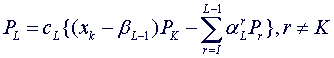 (1.1)
where Pk is a mother term. K and I have to be determined. {PL}
are defined in a finite discrete subset D of (1.1)
where Pk is a mother term. K and I have to be determined. {PL}
are defined in a finite discrete subset D of 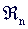 , D={q1,q2,...,qM}.
Every point qj=qj(x1j1,x2j2,...,xnjn) presents a n-coordinate vector
(in this case n=2). The weights, associated with them, wj=1/S2j,
depend on the standard deviation in every point. The points, the weights
and the experimental function values {qj,wj,fjexp}j=1M are given.
The recurrence coefficients { , D={q1,q2,...,qM}.
Every point qj=qj(x1j1,x2j2,...,xnjn) presents a n-coordinate vector
(in this case n=2). The weights, associated with them, wj=1/S2j,
depend on the standard deviation in every point. The points, the weights
and the experimental function values {qj,wj,fjexp}j=1M are given.
The recurrence coefficients {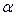 L} and { L} and {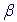 L-1} and normalizing factor {cL}
are evaluated by scalar products of the given values. The description
here follows the descriptions [3,4,7]. In OPEM2 the approximated function
is given by the expansion of the orthonormal polynomials using special
orthonormal coefficients ak. Optimal value of polynomial degree - Lr
is evaluated using two criteria. L-1} and normalizing factor {cL}
are evaluated by scalar products of the given values. The description
here follows the descriptions [3,4,7]. In OPEM2 the approximated function
is given by the expansion of the orthonormal polynomials using special
orthonormal coefficients ak. Optimal value of polynomial degree - Lr
is evaluated using two criteria.
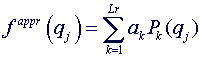 (1.2)
Then orthonormal coefficients {ak} in (1.2) are easily computed by
given values: (1.2)
Then orthonormal coefficients {ak} in (1.2) are easily computed by
given values:
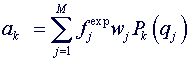 (1.3)
A pyramid of two-dimensional polynomials is given - the hierarchy order
of polynomials in two variables: (1.3)
A pyramid of two-dimensional polynomials is given - the hierarchy order
of polynomials in two variables:
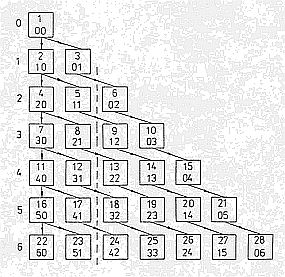 In the cell on the top the number of polynomial is given, and the degrees
j1 and j2 of the x1 and x2 variables also - on the bottom. One example
for evaluating K and I in (1.1) gives for the polynomial P13
(k=2, j1=2, j2=2):
In the cell on the top the number of polynomial is given, and the degrees
j1 and j2 of the x1 and x2 variables also - on the bottom. One example
for evaluating K and I in (1.1) gives for the polynomial P13
(k=2, j1=2, j2=2):
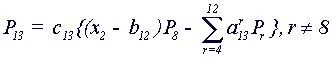 (1.4)
(P8 is a mother term: K=8, I=4).
New theoretical investigations are presented in two-dimensional case in
[7] for the case of differentiation and integration - the fourth member
in the equation (1.1) is added. More detailed description of the
mathematical method with many-dimensional polynomials including
differentiation and integration will be published later in suitable
journal according the description in JINR library with some
implementations.
2.Description of the package OPEM2 (fortran 77)
It consists of main program CALIB and five subroutines:
The principle TSTWO, ORTTWO, PRETWO and 2 auxiliary DEGREE, NUMBER.
The main program CALIB gives:
M - the number of points (nodes);
X and Y - the arrays of coordinates of points;
F - the values of function to be approximated in nodes;
W - the values of weights.
The principal subroutines contain a named common /LINKS/ where
the recurrence factors and auxiliary variables are recorded.
The present size of /LINKS/ allows for overall degrees as high
as 16 and for Lmax=(16+1)(16+2)/2=153. The array dimensions
in /LINKS/ may be changed.
The subroutine TSTWO(X,Y,W,M,F,A,NDEG) is the subroutine,
which calls subprograms. First, it calls PRETWO for preparing
the recurrence factors with overall degree NDEG. Afterwards it
calculates the orthonormal coefficients A, calling the subroutine
ORTTWO. After second call of ORTTWO it calculates the approximating
values and deviations in the points, selects optimal degree Lr,
selects min ( (1.4)
(P8 is a mother term: K=8, I=4).
New theoretical investigations are presented in two-dimensional case in
[7] for the case of differentiation and integration - the fourth member
in the equation (1.1) is added. More detailed description of the
mathematical method with many-dimensional polynomials including
differentiation and integration will be published later in suitable
journal according the description in JINR library with some
implementations.
2.Description of the package OPEM2 (fortran 77)
It consists of main program CALIB and five subroutines:
The principle TSTWO, ORTTWO, PRETWO and 2 auxiliary DEGREE, NUMBER.
The main program CALIB gives:
M - the number of points (nodes);
X and Y - the arrays of coordinates of points;
F - the values of function to be approximated in nodes;
W - the values of weights.
The principal subroutines contain a named common /LINKS/ where
the recurrence factors and auxiliary variables are recorded.
The present size of /LINKS/ allows for overall degrees as high
as 16 and for Lmax=(16+1)(16+2)/2=153. The array dimensions
in /LINKS/ may be changed.
The subroutine TSTWO(X,Y,W,M,F,A,NDEG) is the subroutine,
which calls subprograms. First, it calls PRETWO for preparing
the recurrence factors with overall degree NDEG. Afterwards it
calculates the orthonormal coefficients A, calling the subroutine
ORTTWO. After second call of ORTTWO it calculates the approximating
values and deviations in the points, selects optimal degree Lr,
selects min ( )2, calculates the errors of series coefficients
after third call of ORTTWO and then prints the results.
X and Y - two given one-dimensional arrays of nodes;
W - given weights in every node;
M - given number of points;
F - given function in two dimensions;
A - orthonormal coefficients to be calculated;
NDEG - the max overall degree of polynomials.
The subroutine ORTTWO(NUMBMX,X,Y,POLY) returns the specific values
of all polynomials in an orthonormal series from 1 to NUMBMX at
given values of x and y in POLY-array.
NUMBMX - the value of Lr - optimal degree of polynomials;
X and Y - the coordinates of points, where polynomials are calculated;
POLY - one-dimensional array of results.
The subroutine PRETWO(M,MAXD,X,Y,W,POLY) prepares the recurrence
factors of two-dimensional polynomials, orthonormal over a discrete point
set in a single call, which must precede any working call of ORTTWO.
M - the number of points;
MAXD - the max overall degree for which recurrence factors are
computed (the same as NDEG in TSTWO);
X and Y - two one-dimensional arrays containing the coordinates of points;
W - weights;
POLY - the same as in ORTTWO, and here when computing )2, calculates the errors of series coefficients
after third call of ORTTWO and then prints the results.
X and Y - two given one-dimensional arrays of nodes;
W - given weights in every node;
M - given number of points;
F - given function in two dimensions;
A - orthonormal coefficients to be calculated;
NDEG - the max overall degree of polynomials.
The subroutine ORTTWO(NUMBMX,X,Y,POLY) returns the specific values
of all polynomials in an orthonormal series from 1 to NUMBMX at
given values of x and y in POLY-array.
NUMBMX - the value of Lr - optimal degree of polynomials;
X and Y - the coordinates of points, where polynomials are calculated;
POLY - one-dimensional array of results.
The subroutine PRETWO(M,MAXD,X,Y,W,POLY) prepares the recurrence
factors of two-dimensional polynomials, orthonormal over a discrete point
set in a single call, which must precede any working call of ORTTWO.
M - the number of points;
MAXD - the max overall degree for which recurrence factors are
computed (the same as NDEG in TSTWO);
X and Y - two one-dimensional arrays containing the coordinates of points;
W - weights;
POLY - the same as in ORTTWO, and here when computing  L-1, L-1,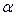 rL and CL.
PRETWO makes successive recursive calls to ORTTWO with NUMBMX = L-1,
then L is incremented, etc, until Lmax is reached.
The subroutine DEGREE(N,J,JX,JY) calculates at given ordinary number
of polynomials N the overall degree of the leading term J, the degree
in x-variable JX, and that in y-variable JY.
The integer function NUMBER(JX,JY) at given x degree JX and
y degree JY returns the ordinary number of polynomials in a series
according to Weisfeld [3] with particular stress on the leading term.
3.Applications
Some applications for receiving calibration coefficients between ideal and
measured grid in the optical devices in HEP are given in [5,6,7].
The last application of the package is for H1 experiment in DESY,
Hamburg - to look for the coordinates of the maximum of the surface
formed by gaussians. The analytic surface over the 400 point's grid
is our approximation. It is done in collaboration with Dubna (LIT).
4.References
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Sources of OPEM2 are submitted. rL and CL.
PRETWO makes successive recursive calls to ORTTWO with NUMBMX = L-1,
then L is incremented, etc, until Lmax is reached.
The subroutine DEGREE(N,J,JX,JY) calculates at given ordinary number
of polynomials N the overall degree of the leading term J, the degree
in x-variable JX, and that in y-variable JY.
The integer function NUMBER(JX,JY) at given x degree JX and
y degree JY returns the ordinary number of polynomials in a series
according to Weisfeld [3] with particular stress on the leading term.
3.Applications
Some applications for receiving calibration coefficients between ideal and
measured grid in the optical devices in HEP are given in [5,6,7].
The last application of the package is for H1 experiment in DESY,
Hamburg - to look for the coordinates of the maximum of the surface
formed by gaussians. The analytic surface over the 400 point's grid
is our approximation. It is done in collaboration with Dubna (LIT).
4.References
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Sources of OPEM2 are submitted.
|
 Author: Nina B.Bogdanova
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) You are
Language: Fortran 77
Author: Nina B.Bogdanova
(Institute of Nuclear Research and Nuclear Energy, BAS,
Tzarigrasko chaussee 72, 1784 Sofia, Bulgaria) You are
Language: Fortran 77  Platform: Windows visitor here.
ORTHONORMAL POLYNOMIAL EXPANSION METHOD IN TWO DIMENSIONS
AND ITS REALIZATION IN FORTRAN PACKAGE OPEM2
A package of Fortran 77 programs is presented. This package has developed
since 1981 for the calibration problems of measurement devices in High
Energy Physics in collaboration with LIT JINR, Dubna.
Last version of the package is developed in part under the contract
of Bulgarian National Council for Sientific Research - Phi 1001.
1.Description of the Method
Orthonormal Polynomial Expansion Method (OPEM2) is the method of
orthogonalization of polynomials based on Householder-Forsythe
3-term relation [1,2] (one-dimensional case) and the Weisfeld
recurrence [3] (many-dimensional case). The recurrence family of
polynomials {PL} is given by:
Platform: Windows visitor here.
ORTHONORMAL POLYNOMIAL EXPANSION METHOD IN TWO DIMENSIONS
AND ITS REALIZATION IN FORTRAN PACKAGE OPEM2
A package of Fortran 77 programs is presented. This package has developed
since 1981 for the calibration problems of measurement devices in High
Energy Physics in collaboration with LIT JINR, Dubna.
Last version of the package is developed in part under the contract
of Bulgarian National Council for Sientific Research - Phi 1001.
1.Description of the Method
Orthonormal Polynomial Expansion Method (OPEM2) is the method of
orthogonalization of polynomials based on Householder-Forsythe
3-term relation [1,2] (one-dimensional case) and the Weisfeld
recurrence [3] (many-dimensional case). The recurrence family of
polynomials {PL} is given by:
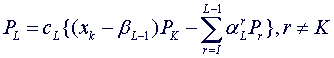 (1.1)
where Pk is a mother term. K and I have to be determined. {PL}
are defined in a finite discrete subset D of
(1.1)
where Pk is a mother term. K and I have to be determined. {PL}
are defined in a finite discrete subset D of 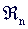 , D={q1,q2,...,qM}.
Every point qj=qj(x1j1,x2j2,...,xnjn) presents a n-coordinate vector
(in this case n=2). The weights, associated with them, wj=1/S2j,
depend on the standard deviation in every point. The points, the weights
and the experimental function values {qj,wj,fjexp}j=1M are given.
The recurrence coefficients {
, D={q1,q2,...,qM}.
Every point qj=qj(x1j1,x2j2,...,xnjn) presents a n-coordinate vector
(in this case n=2). The weights, associated with them, wj=1/S2j,
depend on the standard deviation in every point. The points, the weights
and the experimental function values {qj,wj,fjexp}j=1M are given.
The recurrence coefficients {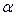 L} and {
L} and {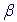 L-1} and normalizing factor {cL}
are evaluated by scalar products of the given values. The description
here follows the descriptions [3,4,7]. In OPEM2 the approximated function
is given by the expansion of the orthonormal polynomials using special
orthonormal coefficients ak. Optimal value of polynomial degree - Lr
is evaluated using two criteria.
L-1} and normalizing factor {cL}
are evaluated by scalar products of the given values. The description
here follows the descriptions [3,4,7]. In OPEM2 the approximated function
is given by the expansion of the orthonormal polynomials using special
orthonormal coefficients ak. Optimal value of polynomial degree - Lr
is evaluated using two criteria.
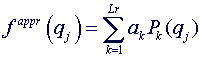 (1.2)
Then orthonormal coefficients {ak} in (1.2) are easily computed by
given values:
(1.2)
Then orthonormal coefficients {ak} in (1.2) are easily computed by
given values:
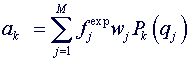 (1.3)
A pyramid of two-dimensional polynomials is given - the hierarchy order
of polynomials in two variables:
(1.3)
A pyramid of two-dimensional polynomials is given - the hierarchy order
of polynomials in two variables:
 In the cell on the top the number of polynomial is given, and the degrees
j1 and j2 of the x1 and x2 variables also - on the bottom. One example
for evaluating K and I in (1.1) gives for the polynomial P13
(k=2, j1=2, j2=2):
In the cell on the top the number of polynomial is given, and the degrees
j1 and j2 of the x1 and x2 variables also - on the bottom. One example
for evaluating K and I in (1.1) gives for the polynomial P13
(k=2, j1=2, j2=2):
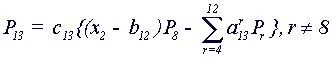 (1.4)
(P8 is a mother term: K=8, I=4).
New theoretical investigations are presented in two-dimensional case in
[7] for the case of differentiation and integration - the fourth member
in the equation (1.1) is added. More detailed description of the
mathematical method with many-dimensional polynomials including
differentiation and integration will be published later in suitable
journal according the description in JINR library with some
implementations.
2.Description of the package OPEM2 (fortran 77)
It consists of main program CALIB and five subroutines:
The principle TSTWO, ORTTWO, PRETWO and 2 auxiliary DEGREE, NUMBER.
The main program CALIB gives:
M - the number of points (nodes);
X and Y - the arrays of coordinates of points;
F - the values of function to be approximated in nodes;
W - the values of weights.
The principal subroutines contain a named common /LINKS/ where
the recurrence factors and auxiliary variables are recorded.
The present size of /LINKS/ allows for overall degrees as high
as 16 and for Lmax=(16+1)(16+2)/2=153. The array dimensions
in /LINKS/ may be changed.
The subroutine TSTWO(X,Y,W,M,F,A,NDEG) is the subroutine,
which calls subprograms. First, it calls PRETWO for preparing
the recurrence factors with overall degree NDEG. Afterwards it
calculates the orthonormal coefficients A, calling the subroutine
ORTTWO. After second call of ORTTWO it calculates the approximating
values and deviations in the points, selects optimal degree Lr,
selects min (
(1.4)
(P8 is a mother term: K=8, I=4).
New theoretical investigations are presented in two-dimensional case in
[7] for the case of differentiation and integration - the fourth member
in the equation (1.1) is added. More detailed description of the
mathematical method with many-dimensional polynomials including
differentiation and integration will be published later in suitable
journal according the description in JINR library with some
implementations.
2.Description of the package OPEM2 (fortran 77)
It consists of main program CALIB and five subroutines:
The principle TSTWO, ORTTWO, PRETWO and 2 auxiliary DEGREE, NUMBER.
The main program CALIB gives:
M - the number of points (nodes);
X and Y - the arrays of coordinates of points;
F - the values of function to be approximated in nodes;
W - the values of weights.
The principal subroutines contain a named common /LINKS/ where
the recurrence factors and auxiliary variables are recorded.
The present size of /LINKS/ allows for overall degrees as high
as 16 and for Lmax=(16+1)(16+2)/2=153. The array dimensions
in /LINKS/ may be changed.
The subroutine TSTWO(X,Y,W,M,F,A,NDEG) is the subroutine,
which calls subprograms. First, it calls PRETWO for preparing
the recurrence factors with overall degree NDEG. Afterwards it
calculates the orthonormal coefficients A, calling the subroutine
ORTTWO. After second call of ORTTWO it calculates the approximating
values and deviations in the points, selects optimal degree Lr,
selects min (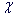 )2, calculates the errors of series coefficients
after third call of ORTTWO and then prints the results.
X and Y - two given one-dimensional arrays of nodes;
W - given weights in every node;
M - given number of points;
F - given function in two dimensions;
A - orthonormal coefficients to be calculated;
NDEG - the max overall degree of polynomials.
The subroutine ORTTWO(NUMBMX,X,Y,POLY) returns the specific values
of all polynomials in an orthonormal series from 1 to NUMBMX at
given values of x and y in POLY-array.
NUMBMX - the value of Lr - optimal degree of polynomials;
X and Y - the coordinates of points, where polynomials are calculated;
POLY - one-dimensional array of results.
The subroutine PRETWO(M,MAXD,X,Y,W,POLY) prepares the recurrence
factors of two-dimensional polynomials, orthonormal over a discrete point
set in a single call, which must precede any working call of ORTTWO.
M - the number of points;
MAXD - the max overall degree for which recurrence factors are
computed (the same as NDEG in TSTWO);
X and Y - two one-dimensional arrays containing the coordinates of points;
W - weights;
POLY - the same as in ORTTWO, and here when computing
)2, calculates the errors of series coefficients
after third call of ORTTWO and then prints the results.
X and Y - two given one-dimensional arrays of nodes;
W - given weights in every node;
M - given number of points;
F - given function in two dimensions;
A - orthonormal coefficients to be calculated;
NDEG - the max overall degree of polynomials.
The subroutine ORTTWO(NUMBMX,X,Y,POLY) returns the specific values
of all polynomials in an orthonormal series from 1 to NUMBMX at
given values of x and y in POLY-array.
NUMBMX - the value of Lr - optimal degree of polynomials;
X and Y - the coordinates of points, where polynomials are calculated;
POLY - one-dimensional array of results.
The subroutine PRETWO(M,MAXD,X,Y,W,POLY) prepares the recurrence
factors of two-dimensional polynomials, orthonormal over a discrete point
set in a single call, which must precede any working call of ORTTWO.
M - the number of points;
MAXD - the max overall degree for which recurrence factors are
computed (the same as NDEG in TSTWO);
X and Y - two one-dimensional arrays containing the coordinates of points;
W - weights;
POLY - the same as in ORTTWO, and here when computing 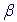 L-1,
L-1,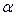 rL and CL.
PRETWO makes successive recursive calls to ORTTWO with NUMBMX = L-1,
then L is incremented, etc, until Lmax is reached.
The subroutine DEGREE(N,J,JX,JY) calculates at given ordinary number
of polynomials N the overall degree of the leading term J, the degree
in x-variable JX, and that in y-variable JY.
The integer function NUMBER(JX,JY) at given x degree JX and
y degree JY returns the ordinary number of polynomials in a series
according to Weisfeld [3] with particular stress on the leading term.
3.Applications
Some applications for receiving calibration coefficients between ideal and
measured grid in the optical devices in HEP are given in [5,6,7].
The last application of the package is for H1 experiment in DESY,
Hamburg - to look for the coordinates of the maximum of the surface
formed by gaussians. The analytic surface over the 400 point's grid
is our approximation. It is done in collaboration with Dubna (LIT).
4.References
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Sources of OPEM2 are submitted.
rL and CL.
PRETWO makes successive recursive calls to ORTTWO with NUMBMX = L-1,
then L is incremented, etc, until Lmax is reached.
The subroutine DEGREE(N,J,JX,JY) calculates at given ordinary number
of polynomials N the overall degree of the leading term J, the degree
in x-variable JX, and that in y-variable JY.
The integer function NUMBER(JX,JY) at given x degree JX and
y degree JY returns the ordinary number of polynomials in a series
according to Weisfeld [3] with particular stress on the leading term.
3.Applications
Some applications for receiving calibration coefficients between ideal and
measured grid in the optical devices in HEP are given in [5,6,7].
The last application of the package is for H1 experiment in DESY,
Hamburg - to look for the coordinates of the maximum of the surface
formed by gaussians. The analytic surface over the 400 point's grid
is our approximation. It is done in collaboration with Dubna (LIT).
4.References
1. A.Householder, Principles of numerical analysis
(Mc Graw-Hill, New York,1953), p.221.
2. G.Forsythe, J.Soc.Ind.Math. 5 (1957) 74.
3. W.Weisfeld, Numer.Math. 1 (1959) 38.
4. V.Gadjokov, Commun.JINR E11-80-782, Dubna (1980).
5. N.Bogdanova, V.Gadjokov, Comp.Phys.Commun.,24 (1981) p.225-229.
6. N.Bogdanova, J.Comp.and Appl.Mathematics, 14 (1986) p.345-351.
7. N.Bogdanova, T.Kupenova, Comp.Phys.Commun.,73 (1992) p.170-178.
Sources of OPEM2 are submitted.