|
TIME6T Библиотека "JINRLIB"  Авторы: С.И.Виницкий, А.А.Гусев, О.Чулуунбаатар Вы
Язык: Фортран
Авторы: С.И.Виницкий, А.А.Гусев, О.Чулуунбаатар Вы
Язык: Фортран  посетитель.
ПАКЕТ ПРОГРАММ НАХОЖДЕНИЯ ЧИСЛЕННЫХ РЕШЕНИЙ ЗАДАЧИ КОШИ
ДЛЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
TIME6T 1.0 - нахождение численных решений
посетитель.
ПАКЕТ ПРОГРАММ НАХОЖДЕНИЯ ЧИСЛЕННЫХ РЕШЕНИЙ ЗАДАЧИ КОШИ
ДЛЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
TIME6T 1.0 - нахождение численных решений 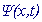 задачи Коши для
нестационарного уравнения Шредингера на конечном интервале задачи Коши для
нестационарного уравнения Шредингера на конечном интервале 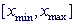 по пространственной переменной.
TIME6T 2.0 - нахождение численных решений
по пространственной переменной.
TIME6T 2.0 - нахождение численных решений 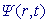 задачи Коши для
многомерного нестационарного уравнения Шредингера.
TIME6T 1.0 - нахождение численных решений задачи Коши для
многомерного нестационарного уравнения Шредингера.
TIME6T 1.0 - нахождение численных решений 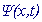 задачи Коши
для нестационарного уравнения Шредингера
на конечном интервале
Подпрограмма TIME6T 1.0 находит численные решения задачи Коши
для нестационарного уравнения Шредингера
на конечном интервале
Подпрограмма TIME6T 1.0 находит численные решения 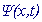 задачи Коши
для нестационарного уравнения Шредингера на конечном интервале задачи Коши
для нестационарного уравнения Шредингера на конечном интервале 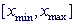 по пространственной переменной
по пространственной переменной
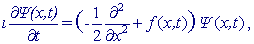 используя явное разложение Магнуса [1] оператора эволюции с дополнительными
калибровочными преобразованиями и его Паде аппроксимации, до порядка
2M (M = 1,2,3) точности по шагу
используя явное разложение Магнуса [1] оператора эволюции с дополнительными
калибровочными преобразованиями и его Паде аппроксимации, до порядка
2M (M = 1,2,3) точности по шагу 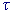 временной переменной t из конечного интер-
вала временной переменной t из конечного интер-
вала 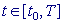 на равномерной сетке на равномерной сетке 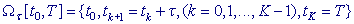 с начальным условием
с начальным условием 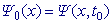 .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [2]. Для аппроксимации используется метод конечных элементов [3]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения.
Литература:
-----------
1. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
2. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
3. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBS, ASSMBM, EMASSD, ESTIFD,ADDVEC,
BOUNDC, COLMHT, ERRDIM, FEGRID,MAXHT, GAULEG,
NODGEN, SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T(TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
1 IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
2 IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой x.
IPRITT - целочисленная переменная, шаг печати решения по временной переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении интер-
вала [x_min,x_max] по пространственной переменой x на подынтервалы:
RMESH(1) = x_min, RMESH(NMESH) = x_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов в
каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках x = x_min и x = x_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются полученные
численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются
значения узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
Пример 1: подпрограмма POTCAL задания потенциальной функции
f(x,t) = (4 - 3 * exp(-t)) * x**2 / 2
SUBROUTINE POTCAL(RG,TT,TAU,DA,HH,DS,SS,ITORDR)
IMPLICIT REAL*8 (A-H,O-Z)
DATA ZERO / 0.D0 /, ONE / 1.D0 /
HH = (4 - 3 * DEXP(-TT)) * RG**2 / 2
SS = ZERO
DA = ONE / 2
DS = ZERO
IF (ITORDR .GE. 2) THEN
F1 = -3 * DEXP(-TT) / 24 * RG**2 / 2
HH = HH + TAU**2 * F1
F1 = 3 * DEXP(-TT) / 12 * RG**2 / 2
SS = SS + TAU**2 * F1
END IF
IF (ITORDR .GE. 3) THEN
F1 = -3 * DEXP(-TT) * RG**2 / 2 / 1920
1 + ( 3 * DEXP(-TT) * RG)**2 / 1440
2 - (-3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
HH = HH + TAU**4 * F1
F1 = 3 * DEXP(-TT) * RG**2 / 2 / 480
1 + (3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
SS = SS + TAU**4 * F1
DA = DA + (- 3 * DEXP(-TT)) * TAU**4 / 720
DS = DS - ( 3 * DEXP(-TT)) * TAU**4 / 720
END IF
RETURN
END
RG - вещественная переменная, значение пространственной переменной x.
TT - вещественная переменная, значение временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
HH - вещественная переменная, содержит часть оператора A^(M)_k без
дифференциального оператора при значении M=ITORDR.
SS - вещественная переменная, содержит часть оператора S^(M)_k без
дифференциального оператора при значении M=ITORDR.
DA - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора A^(M)_k при значении M=ITORDR.
DA = 1/2 при ITORDR = 1 и 2, а DA = 1/2 + f_{xxtt}(x,t) * TAU**4 / 720
при ITORDR = 3.
DS - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора S^(M)_k при значении M=ITORDR.
DS = 0 при ITORDR = 1 и 2, а DS = - f_{xxt}(x,t) * TAU**4 / 720
при ITORDR = 3.
Здесь глобальные переменные RG, TT, TAU задаются главной программой и не
должны изменяться пользователем.
Пример 2: подпрограмма DINIT задания начального условия
psi_0(x) = sqrt(sqrt(1 / pi)) * exp( - (x - sqrt(2))**2 / 2)
SUBROUTINE DINIT(KEY,NN,NGRID,XGRID,ZU1)
IMPLICIT REAL*8 (A-H,O-Y)
IMPLICIT COMPLEX*16 (Z)
DIMENSION ZU1(NN),XGRID(NGRID)
DATA ONE / 1.D0 /, TWO / 2.D0 /
PI = DACOS(- ONE)
FG = DSQRT(DSQRT(ONE / PI))
DO I = 1 , NN
X = XGRID(I + KEY)
ZU1(I) = FG * DEXP( - (X - DSQRT(TWO))**2 / 2)
END DO
RETURN
END
KEY - целочисленная переменная, KEY = 0, если IBOUND >= 3, иначе KEY = 1.
Здесь глобальные переменные KEY, NN, NGRID, XGRID задаются главной
программой и не должны изменяться пользователем.
Примечания:
-----------
1. В подпрограмме TIME6T 1.0 используется динамическое распределение
памяти для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом
примере их размерность задана значениями MTOT=100000, MZTOT=100000,
MITOT=100000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и
выдает диагностику о превышении размерности и указывает, на сколько
их нужно увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляется коэффициент Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 1.0 с подробным описанием, исходными текстами,
примером и результатами.
TIME6T 2.0 - нахождение численных решений .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [2]. Для аппроксимации используется метод конечных элементов [3]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения.
Литература:
-----------
1. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
2. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
3. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBS, ASSMBM, EMASSD, ESTIFD,ADDVEC,
BOUNDC, COLMHT, ERRDIM, FEGRID,MAXHT, GAULEG,
NODGEN, SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T(TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
1 IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
2 IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой x.
IPRITT - целочисленная переменная, шаг печати решения по временной переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении интер-
вала [x_min,x_max] по пространственной переменой x на подынтервалы:
RMESH(1) = x_min, RMESH(NMESH) = x_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов в
каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках x = x_min и x = x_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются полученные
численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются
значения узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
Пример 1: подпрограмма POTCAL задания потенциальной функции
f(x,t) = (4 - 3 * exp(-t)) * x**2 / 2
SUBROUTINE POTCAL(RG,TT,TAU,DA,HH,DS,SS,ITORDR)
IMPLICIT REAL*8 (A-H,O-Z)
DATA ZERO / 0.D0 /, ONE / 1.D0 /
HH = (4 - 3 * DEXP(-TT)) * RG**2 / 2
SS = ZERO
DA = ONE / 2
DS = ZERO
IF (ITORDR .GE. 2) THEN
F1 = -3 * DEXP(-TT) / 24 * RG**2 / 2
HH = HH + TAU**2 * F1
F1 = 3 * DEXP(-TT) / 12 * RG**2 / 2
SS = SS + TAU**2 * F1
END IF
IF (ITORDR .GE. 3) THEN
F1 = -3 * DEXP(-TT) * RG**2 / 2 / 1920
1 + ( 3 * DEXP(-TT) * RG)**2 / 1440
2 - (-3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
HH = HH + TAU**4 * F1
F1 = 3 * DEXP(-TT) * RG**2 / 2 / 480
1 + (3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
SS = SS + TAU**4 * F1
DA = DA + (- 3 * DEXP(-TT)) * TAU**4 / 720
DS = DS - ( 3 * DEXP(-TT)) * TAU**4 / 720
END IF
RETURN
END
RG - вещественная переменная, значение пространственной переменной x.
TT - вещественная переменная, значение временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
HH - вещественная переменная, содержит часть оператора A^(M)_k без
дифференциального оператора при значении M=ITORDR.
SS - вещественная переменная, содержит часть оператора S^(M)_k без
дифференциального оператора при значении M=ITORDR.
DA - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора A^(M)_k при значении M=ITORDR.
DA = 1/2 при ITORDR = 1 и 2, а DA = 1/2 + f_{xxtt}(x,t) * TAU**4 / 720
при ITORDR = 3.
DS - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора S^(M)_k при значении M=ITORDR.
DS = 0 при ITORDR = 1 и 2, а DS = - f_{xxt}(x,t) * TAU**4 / 720
при ITORDR = 3.
Здесь глобальные переменные RG, TT, TAU задаются главной программой и не
должны изменяться пользователем.
Пример 2: подпрограмма DINIT задания начального условия
psi_0(x) = sqrt(sqrt(1 / pi)) * exp( - (x - sqrt(2))**2 / 2)
SUBROUTINE DINIT(KEY,NN,NGRID,XGRID,ZU1)
IMPLICIT REAL*8 (A-H,O-Y)
IMPLICIT COMPLEX*16 (Z)
DIMENSION ZU1(NN),XGRID(NGRID)
DATA ONE / 1.D0 /, TWO / 2.D0 /
PI = DACOS(- ONE)
FG = DSQRT(DSQRT(ONE / PI))
DO I = 1 , NN
X = XGRID(I + KEY)
ZU1(I) = FG * DEXP( - (X - DSQRT(TWO))**2 / 2)
END DO
RETURN
END
KEY - целочисленная переменная, KEY = 0, если IBOUND >= 3, иначе KEY = 1.
Здесь глобальные переменные KEY, NN, NGRID, XGRID задаются главной
программой и не должны изменяться пользователем.
Примечания:
-----------
1. В подпрограмме TIME6T 1.0 используется динамическое распределение
памяти для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом
примере их размерность задана значениями MTOT=100000, MZTOT=100000,
MITOT=100000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и
выдает диагностику о превышении размерности и указывает, на сколько
их нужно увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляется коэффициент Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 1.0 с подробным описанием, исходными текстами,
примером и результатами.
TIME6T 2.0 - нахождение численных решений 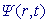 задачи Коши
для многомерного нестационарного уравнения Шредингера
Подпрограмма TIME6T 2.0 находит численные решения задачи Коши
для многомерного нестационарного уравнения Шредингера
Подпрограмма TIME6T 2.0 находит численные решения 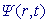 задачи Коши
для нестационарного уравнения Шредингера в d-мерном пространстве задачи Коши
для нестационарного уравнения Шредингера в d-мерном пространстве
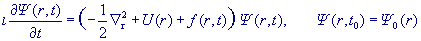 в рамках метода Канторовича [1], используя явное разложение Магнуса [2]
оператора эволюции с дополнительными калибровочными преобразованиями и его
Паде аппроксимации, до порядка 2M (M = 1,2,3) точности по шагу
в рамках метода Канторовича [1], используя явное разложение Магнуса [2]
оператора эволюции с дополнительными калибровочными преобразованиями и его
Паде аппроксимации, до порядка 2M (M = 1,2,3) точности по шагу 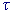 временной
переменной t из конечного интервала временной
переменной t из конечного интервала 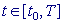 на равномерной сетке на равномерной сетке
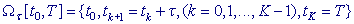 .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [3]. Для аппроксимации используется метод конечных элементов [4]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения. Тестовый пример взят из работы [5].
Литература:
-----------
1. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа.
Москва, Гостехиздат, 1952.
2. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
3. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
4. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
5. Chuluunbaatar O. et al. Phys. Rev E ,2008, v.78, pp. 017702-1-4.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBN, ASSMBT, EMASSD, ESTIFD, ESTIFN,
ESTITD, ESTITN, ADDVEC, HQPOTN, SGPOTN, BOUNDC,
COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN,
SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, POTTIM, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T (TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
1 IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
2 IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
3 IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
MDIM - целая переменная, число уравнений.
IDIM - целая переменная, размерность пространства.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой r.
IPRITT - целочисленная переменная, шаг печати решения по временной
переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении
интервала [0,r_max] по пространственной переменой r на подынтервалы:
RMESH(1) = r, RMESH(NMESH) = r_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов
в каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках r = 0 и r = r_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются
полученные численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
POTEN - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUP - целочисленная переменная, номер выходного логического устройства POTEN.
POTTM - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUD - целочисленная переменная, номер выходного логического устройства POTTM.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются значения
узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
В подпрограмме POTCAL задаются потенциальные матрицы V, Q.
В подпрограмме POTTIM задаются потенциальные матрицы G, Z.
В подпрограмме DINIT задается начальное условие.
Примечания:
-----------
1. В подпрограмме TIME6T 2.0 используется динамическое распределение памяти
для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом примере их
размерность задана значениями MTOT=2 000 000, MZTOT=1 000 000,
MITOT=300 000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и выдает
диагностику о превышении размерности и указывает, на сколько их нужно
увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляются коэффициенты Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 2.0 с подробным описанием, исходными текстами,
примером и результатами. .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [3]. Для аппроксимации используется метод конечных элементов [4]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения. Тестовый пример взят из работы [5].
Литература:
-----------
1. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа.
Москва, Гостехиздат, 1952.
2. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
3. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
4. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
5. Chuluunbaatar O. et al. Phys. Rev E ,2008, v.78, pp. 017702-1-4.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBN, ASSMBT, EMASSD, ESTIFD, ESTIFN,
ESTITD, ESTITN, ADDVEC, HQPOTN, SGPOTN, BOUNDC,
COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN,
SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, POTTIM, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T (TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
1 IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
2 IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
3 IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
MDIM - целая переменная, число уравнений.
IDIM - целая переменная, размерность пространства.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой r.
IPRITT - целочисленная переменная, шаг печати решения по временной
переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении
интервала [0,r_max] по пространственной переменой r на подынтервалы:
RMESH(1) = r, RMESH(NMESH) = r_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов
в каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках r = 0 и r = r_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются
полученные численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
POTEN - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUP - целочисленная переменная, номер выходного логического устройства POTEN.
POTTM - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUD - целочисленная переменная, номер выходного логического устройства POTTM.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются значения
узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
В подпрограмме POTCAL задаются потенциальные матрицы V, Q.
В подпрограмме POTTIM задаются потенциальные матрицы G, Z.
В подпрограмме DINIT задается начальное условие.
Примечания:
-----------
1. В подпрограмме TIME6T 2.0 используется динамическое распределение памяти
для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом примере их
размерность задана значениями MTOT=2 000 000, MZTOT=1 000 000,
MITOT=300 000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и выдает
диагностику о превышении размерности и указывает, на сколько их нужно
увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляются коэффициенты Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 2.0 с подробным описанием, исходными текстами,
примером и результатами.
|
 Авторы: С.И.Виницкий, А.А.Гусев, О.Чулуунбаатар Вы
Язык: Фортран
Авторы: С.И.Виницкий, А.А.Гусев, О.Чулуунбаатар Вы
Язык: Фортран  посетитель.
ПАКЕТ ПРОГРАММ НАХОЖДЕНИЯ ЧИСЛЕННЫХ РЕШЕНИЙ ЗАДАЧИ КОШИ
ДЛЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
TIME6T 1.0 - нахождение численных решений
посетитель.
ПАКЕТ ПРОГРАММ НАХОЖДЕНИЯ ЧИСЛЕННЫХ РЕШЕНИЙ ЗАДАЧИ КОШИ
ДЛЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
TIME6T 1.0 - нахождение численных решений 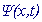 задачи Коши для
нестационарного уравнения Шредингера на конечном интервале
задачи Коши для
нестационарного уравнения Шредингера на конечном интервале 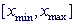 по пространственной переменной.
TIME6T 2.0 - нахождение численных решений
по пространственной переменной.
TIME6T 2.0 - нахождение численных решений 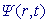 задачи Коши для
многомерного нестационарного уравнения Шредингера.
TIME6T 1.0 - нахождение численных решений
задачи Коши для
многомерного нестационарного уравнения Шредингера.
TIME6T 1.0 - нахождение численных решений 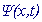 задачи Коши
для нестационарного уравнения Шредингера
на конечном интервале
Подпрограмма TIME6T 1.0 находит численные решения
задачи Коши
для нестационарного уравнения Шредингера
на конечном интервале
Подпрограмма TIME6T 1.0 находит численные решения 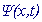 задачи Коши
для нестационарного уравнения Шредингера на конечном интервале
задачи Коши
для нестационарного уравнения Шредингера на конечном интервале 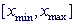 по пространственной переменной
по пространственной переменной
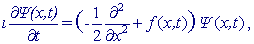 используя явное разложение Магнуса [1] оператора эволюции с дополнительными
калибровочными преобразованиями и его Паде аппроксимации, до порядка
2M (M = 1,2,3) точности по шагу
используя явное разложение Магнуса [1] оператора эволюции с дополнительными
калибровочными преобразованиями и его Паде аппроксимации, до порядка
2M (M = 1,2,3) точности по шагу 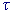 временной переменной t из конечного интер-
вала
временной переменной t из конечного интер-
вала 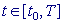 на равномерной сетке
на равномерной сетке 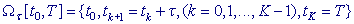 с начальным условием
с начальным условием 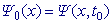 .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [2]. Для аппроксимации используется метод конечных элементов [3]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения.
Литература:
-----------
1. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
2. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
3. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBS, ASSMBM, EMASSD, ESTIFD,ADDVEC,
BOUNDC, COLMHT, ERRDIM, FEGRID,MAXHT, GAULEG,
NODGEN, SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T(TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
1 IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
2 IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой x.
IPRITT - целочисленная переменная, шаг печати решения по временной переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении интер-
вала [x_min,x_max] по пространственной переменой x на подынтервалы:
RMESH(1) = x_min, RMESH(NMESH) = x_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов в
каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках x = x_min и x = x_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются полученные
численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются
значения узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
Пример 1: подпрограмма POTCAL задания потенциальной функции
f(x,t) = (4 - 3 * exp(-t)) * x**2 / 2
SUBROUTINE POTCAL(RG,TT,TAU,DA,HH,DS,SS,ITORDR)
IMPLICIT REAL*8 (A-H,O-Z)
DATA ZERO / 0.D0 /, ONE / 1.D0 /
HH = (4 - 3 * DEXP(-TT)) * RG**2 / 2
SS = ZERO
DA = ONE / 2
DS = ZERO
IF (ITORDR .GE. 2) THEN
F1 = -3 * DEXP(-TT) / 24 * RG**2 / 2
HH = HH + TAU**2 * F1
F1 = 3 * DEXP(-TT) / 12 * RG**2 / 2
SS = SS + TAU**2 * F1
END IF
IF (ITORDR .GE. 3) THEN
F1 = -3 * DEXP(-TT) * RG**2 / 2 / 1920
1 + ( 3 * DEXP(-TT) * RG)**2 / 1440
2 - (-3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
HH = HH + TAU**4 * F1
F1 = 3 * DEXP(-TT) * RG**2 / 2 / 480
1 + (3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
SS = SS + TAU**4 * F1
DA = DA + (- 3 * DEXP(-TT)) * TAU**4 / 720
DS = DS - ( 3 * DEXP(-TT)) * TAU**4 / 720
END IF
RETURN
END
RG - вещественная переменная, значение пространственной переменной x.
TT - вещественная переменная, значение временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
HH - вещественная переменная, содержит часть оператора A^(M)_k без
дифференциального оператора при значении M=ITORDR.
SS - вещественная переменная, содержит часть оператора S^(M)_k без
дифференциального оператора при значении M=ITORDR.
DA - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора A^(M)_k при значении M=ITORDR.
DA = 1/2 при ITORDR = 1 и 2, а DA = 1/2 + f_{xxtt}(x,t) * TAU**4 / 720
при ITORDR = 3.
DS - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора S^(M)_k при значении M=ITORDR.
DS = 0 при ITORDR = 1 и 2, а DS = - f_{xxt}(x,t) * TAU**4 / 720
при ITORDR = 3.
Здесь глобальные переменные RG, TT, TAU задаются главной программой и не
должны изменяться пользователем.
Пример 2: подпрограмма DINIT задания начального условия
psi_0(x) = sqrt(sqrt(1 / pi)) * exp( - (x - sqrt(2))**2 / 2)
SUBROUTINE DINIT(KEY,NN,NGRID,XGRID,ZU1)
IMPLICIT REAL*8 (A-H,O-Y)
IMPLICIT COMPLEX*16 (Z)
DIMENSION ZU1(NN),XGRID(NGRID)
DATA ONE / 1.D0 /, TWO / 2.D0 /
PI = DACOS(- ONE)
FG = DSQRT(DSQRT(ONE / PI))
DO I = 1 , NN
X = XGRID(I + KEY)
ZU1(I) = FG * DEXP( - (X - DSQRT(TWO))**2 / 2)
END DO
RETURN
END
KEY - целочисленная переменная, KEY = 0, если IBOUND >= 3, иначе KEY = 1.
Здесь глобальные переменные KEY, NN, NGRID, XGRID задаются главной
программой и не должны изменяться пользователем.
Примечания:
-----------
1. В подпрограмме TIME6T 1.0 используется динамическое распределение
памяти для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом
примере их размерность задана значениями MTOT=100000, MZTOT=100000,
MITOT=100000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и
выдает диагностику о превышении размерности и указывает, на сколько
их нужно увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляется коэффициент Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 1.0 с подробным описанием, исходными текстами,
примером и результатами.
TIME6T 2.0 - нахождение численных решений
.
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [2]. Для аппроксимации используется метод конечных элементов [3]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения.
Литература:
-----------
1. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
2. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
3. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBS, ASSMBM, EMASSD, ESTIFD,ADDVEC,
BOUNDC, COLMHT, ERRDIM, FEGRID,MAXHT, GAULEG,
NODGEN, SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T(TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
1 IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
2 IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,
IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,
IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой x.
IPRITT - целочисленная переменная, шаг печати решения по временной переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении интер-
вала [x_min,x_max] по пространственной переменой x на подынтервалы:
RMESH(1) = x_min, RMESH(NMESH) = x_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов в
каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках x = x_min и x = x_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются полученные
численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются
значения узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
Пример 1: подпрограмма POTCAL задания потенциальной функции
f(x,t) = (4 - 3 * exp(-t)) * x**2 / 2
SUBROUTINE POTCAL(RG,TT,TAU,DA,HH,DS,SS,ITORDR)
IMPLICIT REAL*8 (A-H,O-Z)
DATA ZERO / 0.D0 /, ONE / 1.D0 /
HH = (4 - 3 * DEXP(-TT)) * RG**2 / 2
SS = ZERO
DA = ONE / 2
DS = ZERO
IF (ITORDR .GE. 2) THEN
F1 = -3 * DEXP(-TT) / 24 * RG**2 / 2
HH = HH + TAU**2 * F1
F1 = 3 * DEXP(-TT) / 12 * RG**2 / 2
SS = SS + TAU**2 * F1
END IF
IF (ITORDR .GE. 3) THEN
F1 = -3 * DEXP(-TT) * RG**2 / 2 / 1920
1 + ( 3 * DEXP(-TT) * RG)**2 / 1440
2 - (-3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
HH = HH + TAU**4 * F1
F1 = 3 * DEXP(-TT) * RG**2 / 2 / 480
1 + (3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
SS = SS + TAU**4 * F1
DA = DA + (- 3 * DEXP(-TT)) * TAU**4 / 720
DS = DS - ( 3 * DEXP(-TT)) * TAU**4 / 720
END IF
RETURN
END
RG - вещественная переменная, значение пространственной переменной x.
TT - вещественная переменная, значение временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
HH - вещественная переменная, содержит часть оператора A^(M)_k без
дифференциального оператора при значении M=ITORDR.
SS - вещественная переменная, содержит часть оператора S^(M)_k без
дифференциального оператора при значении M=ITORDR.
DA - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора A^(M)_k при значении M=ITORDR.
DA = 1/2 при ITORDR = 1 и 2, а DA = 1/2 + f_{xxtt}(x,t) * TAU**4 / 720
при ITORDR = 3.
DS - вещественная переменная, содержит коэффициенты при дифференциальных
операторах оператора S^(M)_k при значении M=ITORDR.
DS = 0 при ITORDR = 1 и 2, а DS = - f_{xxt}(x,t) * TAU**4 / 720
при ITORDR = 3.
Здесь глобальные переменные RG, TT, TAU задаются главной программой и не
должны изменяться пользователем.
Пример 2: подпрограмма DINIT задания начального условия
psi_0(x) = sqrt(sqrt(1 / pi)) * exp( - (x - sqrt(2))**2 / 2)
SUBROUTINE DINIT(KEY,NN,NGRID,XGRID,ZU1)
IMPLICIT REAL*8 (A-H,O-Y)
IMPLICIT COMPLEX*16 (Z)
DIMENSION ZU1(NN),XGRID(NGRID)
DATA ONE / 1.D0 /, TWO / 2.D0 /
PI = DACOS(- ONE)
FG = DSQRT(DSQRT(ONE / PI))
DO I = 1 , NN
X = XGRID(I + KEY)
ZU1(I) = FG * DEXP( - (X - DSQRT(TWO))**2 / 2)
END DO
RETURN
END
KEY - целочисленная переменная, KEY = 0, если IBOUND >= 3, иначе KEY = 1.
Здесь глобальные переменные KEY, NN, NGRID, XGRID задаются главной
программой и не должны изменяться пользователем.
Примечания:
-----------
1. В подпрограмме TIME6T 1.0 используется динамическое распределение
памяти для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом
примере их размерность задана значениями MTOT=100000, MZTOT=100000,
MITOT=100000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и
выдает диагностику о превышении размерности и указывает, на сколько
их нужно увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляется коэффициент Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 1.0 с подробным описанием, исходными текстами,
примером и результатами.
TIME6T 2.0 - нахождение численных решений 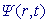 задачи Коши
для многомерного нестационарного уравнения Шредингера
Подпрограмма TIME6T 2.0 находит численные решения
задачи Коши
для многомерного нестационарного уравнения Шредингера
Подпрограмма TIME6T 2.0 находит численные решения 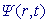 задачи Коши
для нестационарного уравнения Шредингера в d-мерном пространстве
задачи Коши
для нестационарного уравнения Шредингера в d-мерном пространстве
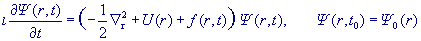 в рамках метода Канторовича [1], используя явное разложение Магнуса [2]
оператора эволюции с дополнительными калибровочными преобразованиями и его
Паде аппроксимации, до порядка 2M (M = 1,2,3) точности по шагу
в рамках метода Канторовича [1], используя явное разложение Магнуса [2]
оператора эволюции с дополнительными калибровочными преобразованиями и его
Паде аппроксимации, до порядка 2M (M = 1,2,3) точности по шагу 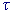 временной
переменной t из конечного интервала
временной
переменной t из конечного интервала 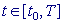 на равномерной сетке
на равномерной сетке
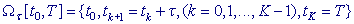 .
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [3]. Для аппроксимации используется метод конечных элементов [4]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения. Тестовый пример взят из работы [5].
Литература:
-----------
1. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа.
Москва, Гостехиздат, 1952.
2. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
3. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
4. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
5. Chuluunbaatar O. et al. Phys. Rev E ,2008, v.78, pp. 017702-1-4.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBN, ASSMBT, EMASSD, ESTIFD, ESTIFN,
ESTITD, ESTITN, ADDVEC, HQPOTN, SGPOTN, BOUNDC,
COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN,
SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, POTTIM, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T (TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
1 IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
2 IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
3 IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
MDIM - целая переменная, число уравнений.
IDIM - целая переменная, размерность пространства.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой r.
IPRITT - целочисленная переменная, шаг печати решения по временной
переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении
интервала [0,r_max] по пространственной переменой r на подынтервалы:
RMESH(1) = r, RMESH(NMESH) = r_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов
в каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках r = 0 и r = r_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются
полученные численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
POTEN - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUP - целочисленная переменная, номер выходного логического устройства POTEN.
POTTM - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUD - целочисленная переменная, номер выходного логического устройства POTTM.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются значения
узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
В подпрограмме POTCAL задаются потенциальные матрицы V, Q.
В подпрограмме POTTIM задаются потенциальные матрицы G, Z.
В подпрограмме DINIT задается начальное условие.
Примечания:
-----------
1. В подпрограмме TIME6T 2.0 используется динамическое распределение памяти
для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом примере их
размерность задана значениями MTOT=2 000 000, MZTOT=1 000 000,
MITOT=300 000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и выдает
диагностику о превышении размерности и указывает, на сколько их нужно
увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляются коэффициенты Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 2.0 с подробным описанием, исходными текстами,
примером и результатами.
.
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [3]. Для аппроксимации используется метод конечных элементов [4]
с интерполяционными полиномами Лагранжа до порядка p=8 при подходящей
гладкости решения. Тестовый пример взят из работы [5].
Литература:
-----------
1. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа.
Москва, Гостехиздат, 1952.
2. Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
3. Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
4. Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
5. Chuluunbaatar O. et al. Phys. Rev E ,2008, v.78, pp. 017702-1-4.
Структура:
----------
SUBROUTINE
Имя: TIME6T
Внутренние подпрограммы: TMSOLV, ASSMBN, ASSMBT, EMASSD, ESTIFD, ESTIFN,
ESTITD, ESTITN, ADDVEC, HQPOTN, SGPOTN, BOUNDC,
COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN,
SHAPEF, MULTC, MULTCC, REDBAC, DECOMC
Внешние подпрограммы: POTCAL, POTTIM, DINIT (составляются пользователем)
Обращение:
----------
CALL TIME6T (TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
1 IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
2 IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
3 IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,
IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,
IOUT,POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,
IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT:
TITLE - символьная переменная, название рабочего варианта программы.
MDIM - целая переменная, число уравнений.
IDIM - целая переменная, размерность пространства.
NPOL - целая переменная, порядок интерполяционных полиномов Лагранжа.
TMIN - вещественная переменная, начальная точка временного интервала.
TMAX - вещественная переменная, конечная точка временного интервала.
TAU - вещественная переменная, шаг по временной переменной t.
ITORDR - целочисленная переменная, принимающая значения 1-3, порядок
разложения Магнуса.
IPRINT - целочисленная переменная, принимающая значения 0-2, уровень печати
результатов.
IPRSTP - целочисленная переменная, шаг печати решения по пространственной
переменой r.
IPRITT - целочисленная переменная, шаг печати решения по временной
переменой t.
NMESH - целочисленная переменная, размерность массива RMESH. Значение
NMESH всегда >= 3 и нечетное.
RMESH - вещественный массив, массив RMESH содержит информацию о делении
интервала [0,r_max] по пространственной переменой r на подынтервалы:
RMESH(1) = r, RMESH(NMESH) = r_max, и значения
RMESH(I), I=2, 4, ... , NMESH-1, устанавливается число элементов
в каждом подынтервале [RMESH(I-1), RMESH(I+1)].
IBOUND - целочисленная переменная, параметр, задающий тип краевых условий
в граничных точках r = 0 и r = r_max:
= 1 - Дирихле - Дирихле;
= 2 - Дирихле - Нейман;
= 3 - Нейман - Дирихле;
= 4 - Нейман - Нейман.
FNOUT - символьная переменная, название файла, в котором печатаются
полученные численные результаты.
IOUT - целочисленная переменная, номер выходного логического устройства FNOUT.
POTEN - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUP - целочисленная переменная, номер выходного логического устройства POTEN.
POTTM - символьная переменная, название файла, в котором хранятся значения
используемых потенциальных матриц.
IOUD - целочисленная переменная, номер выходного логического устройства POTTM.
FMATR - символьная переменная, название файла, в котором хранятся значения
используемых матриц.
IOUM - целочисленная переменная, номер выходного логического устройства FMATR.
EVWFN - символьная переменная, название файла, в котором печатаются значения
узловых точек и полученные численные решения в этих точках.
Эта опция используется только, если IOUF > 0.
IOUF - целочисленная переменная, номер выходного логического устройства EVWFN.
TOT - вещественный массив, рабочий вектор.
ITOT - целочисленный массив, рабочий вектор.
ZTOT - комплексный массив, рабочий вектор.
MTOT - целочисленная переменная, размерность массива TOT.
MITOT - целочисленная переменная, размерность массива ITOT.
MZTOT - целочисленная переменная, размерность массива ZTOT.
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
NGRID - целочисленная переменная, число конечно-элементных узлов.
NN - целочисленная переменная, число конечно-элементных узлов численного
решения.
TT - вещественная переменная, значения временной переменной t.
TAU - вещественная переменная, шаг по временной переменной t.
XGRID - вещественный массив, содержащий значения конечно-элементных узлов.
ZU - комплексный массив, содержащий вычисленное решение.
В подпрограмме POTCAL задаются потенциальные матрицы V, Q.
В подпрограмме POTTIM задаются потенциальные матрицы G, Z.
В подпрограмме DINIT задается начальное условие.
Примечания:
-----------
1. В подпрограмме TIME6T 2.0 используется динамическое распределение памяти
для одномерных массивов TOT, ZTOT, ITOT, RMESH. В тестовом примере их
размерность задана значениями MTOT=2 000 000, MZTOT=1 000 000,
MITOT=300 000, NMESH1=5. Если пользователь задал недостаточные значения
размерности вышеуказанных массивов, то программа останавливается и выдает
диагностику о превышении размерности и указывает, на сколько их нужно
увеличить.
2. Для контроля точности численного решения по шагу TAU дополнительно
вычисляются коэффициенты Рунге на четырех вдвое сгущающихся сетках
с помощью подпрограммы RUNGE.
Архив программы TIME6T 2.0 с подробным описанием, исходными текстами,
примером и результатами.



