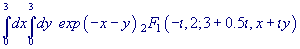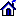|
ZHYPG2 Library "JINRLIB"  Author: O.Chuluunbaatar You are
Language: Fortran
Author: O.Chuluunbaatar You are
Language: Fortran  visitor here.
Calculation of the hypergeometric functions
visitor here.
Calculation of the hypergeometric functions 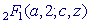 with complex parameters and complex argument
The function ZHYPG2 computes the hypergeometric functions
with complex parameters and complex argument
The function ZHYPG2 computes the hypergeometric functions 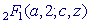 with
complex parameters with
complex parameters  , , 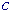 and an argument and an argument 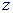 [1]. For calculation of the
hypergeometric function [1]. For calculation of the
hypergeometric function 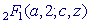 it used the beforehand calculated values
of the hypergeometric functions and their derivatives by means of the
subroutine HYPGEO [2] at points it used the beforehand calculated values
of the hypergeometric functions and their derivatives by means of the
subroutine HYPGEO [2] at points
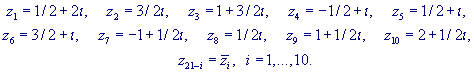 The considered procedure was constructed on the basis of the algorithms
published in [3]. The described algorithm allows one to save calculation
time of the multidimensional integrals, whose kernel contains hypergeometric
functions
The considered procedure was constructed on the basis of the algorithms
published in [3]. The described algorithm allows one to save calculation
time of the multidimensional integrals, whose kernel contains hypergeometric
functions 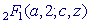 , approximately 10-60 times depending on accuracy of
the calculation (10-4-10-14) in comparison with a direct use of the subroutine
HYPGEO at each value , approximately 10-60 times depending on accuracy of
the calculation (10-4-10-14) in comparison with a direct use of the subroutine
HYPGEO at each value 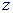 . This type of calculations occurs in investigation
of the single and double ionizations by electron impact of two-nuclear
molecules (see papers [4,5]).
References:
-----------
1. Abramowitz M. and Stegun I. Handbook of mathematical functions,
National Bureau of Standards Applied Mathematics series. 55. 1964.
2. Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P.
Numerical recipes: The art of scientific computing.
Cambridge University Press, Cambridge, 1986.
3. Chuluunbaatar O. Bulletin of Tver State University:
Ser. Applied Mathematics. 2008, N = 26(86), pp. 47-64.
4. Chuluunbaatar O., Joulakian B.B., Tsookhuu Kh. and Vinitsky S.I.
J. Phys. B, 2004, v. 37, pp. 2607-2616.
5. Chuluunbaatar O., Joulakian B.B., Puzynin I.V., Tsookhuu Kh. and
Vinitsky S.I. J. Phys. B, 2008, v. 41, pp.015204-1-6.
Structure:
----------
FUNCTION
Name: ZHYPG2
Internal subroutines: ZSUM, ZGAMMA, DRHYP, CGAMA, HYPGEO, HYPDRV,
HYPSER, ODEINT, BSSTEP, MMID, PZEXTR
Usage:
------
ZFUNC = ZHYPG2(ZA,ZC,ZZ,NMAX,EPS)
INPUT: ZA, ZC, ZZ, NMAX, EPS:
ZA - double complex number, contains value of parameter . This type of calculations occurs in investigation
of the single and double ionizations by electron impact of two-nuclear
molecules (see papers [4,5]).
References:
-----------
1. Abramowitz M. and Stegun I. Handbook of mathematical functions,
National Bureau of Standards Applied Mathematics series. 55. 1964.
2. Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P.
Numerical recipes: The art of scientific computing.
Cambridge University Press, Cambridge, 1986.
3. Chuluunbaatar O. Bulletin of Tver State University:
Ser. Applied Mathematics. 2008, N = 26(86), pp. 47-64.
4. Chuluunbaatar O., Joulakian B.B., Tsookhuu Kh. and Vinitsky S.I.
J. Phys. B, 2004, v. 37, pp. 2607-2616.
5. Chuluunbaatar O., Joulakian B.B., Puzynin I.V., Tsookhuu Kh. and
Vinitsky S.I. J. Phys. B, 2008, v. 41, pp.015204-1-6.
Structure:
----------
FUNCTION
Name: ZHYPG2
Internal subroutines: ZSUM, ZGAMMA, DRHYP, CGAMA, HYPGEO, HYPDRV,
HYPSER, ODEINT, BSSTEP, MMID, PZEXTR
Usage:
------
ZFUNC = ZHYPG2(ZA,ZC,ZZ,NMAX,EPS)
INPUT: ZA, ZC, ZZ, NMAX, EPS:
ZA - double complex number, contains value of parameter  ZC - double complex number, contains value of parameter
ZC - double complex number, contains value of parameter 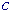 .
ZZ - double complex number, contains value of argument .
ZZ - double complex number, contains value of argument 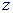 .
NMAX - integer number, the maximum number of summation of truncated
Gaussian series.
EPS - double precision number, given accuracy.
Sources with example and description are submitted.
Example: .
NMAX - integer number, the maximum number of summation of truncated
Gaussian series.
EPS - double precision number, given accuracy.
Sources with example and description are submitted.
Example:
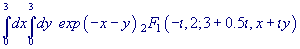
|
 Author: O.Chuluunbaatar You are
Language: Fortran
Author: O.Chuluunbaatar You are
Language: Fortran  visitor here.
Calculation of the hypergeometric functions
visitor here.
Calculation of the hypergeometric functions 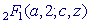 with complex parameters and complex argument
The function ZHYPG2 computes the hypergeometric functions
with complex parameters and complex argument
The function ZHYPG2 computes the hypergeometric functions 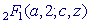 with
complex parameters
with
complex parameters  ,
, 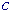 and an argument
and an argument 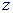 [1]. For calculation of the
hypergeometric function
[1]. For calculation of the
hypergeometric function 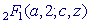 it used the beforehand calculated values
of the hypergeometric functions and their derivatives by means of the
subroutine HYPGEO [2] at points
it used the beforehand calculated values
of the hypergeometric functions and their derivatives by means of the
subroutine HYPGEO [2] at points
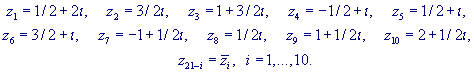 The considered procedure was constructed on the basis of the algorithms
published in [3]. The described algorithm allows one to save calculation
time of the multidimensional integrals, whose kernel contains hypergeometric
functions
The considered procedure was constructed on the basis of the algorithms
published in [3]. The described algorithm allows one to save calculation
time of the multidimensional integrals, whose kernel contains hypergeometric
functions 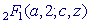 , approximately 10-60 times depending on accuracy of
the calculation (10-4-10-14) in comparison with a direct use of the subroutine
HYPGEO at each value
, approximately 10-60 times depending on accuracy of
the calculation (10-4-10-14) in comparison with a direct use of the subroutine
HYPGEO at each value 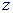 . This type of calculations occurs in investigation
of the single and double ionizations by electron impact of two-nuclear
molecules (see papers [4,5]).
References:
-----------
1. Abramowitz M. and Stegun I. Handbook of mathematical functions,
National Bureau of Standards Applied Mathematics series. 55. 1964.
2. Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P.
Numerical recipes: The art of scientific computing.
Cambridge University Press, Cambridge, 1986.
3. Chuluunbaatar O. Bulletin of Tver State University:
Ser. Applied Mathematics. 2008, N = 26(86), pp. 47-64.
4. Chuluunbaatar O., Joulakian B.B., Tsookhuu Kh. and Vinitsky S.I.
J. Phys. B, 2004, v. 37, pp. 2607-2616.
5. Chuluunbaatar O., Joulakian B.B., Puzynin I.V., Tsookhuu Kh. and
Vinitsky S.I. J. Phys. B, 2008, v. 41, pp.015204-1-6.
Structure:
----------
FUNCTION
Name: ZHYPG2
Internal subroutines: ZSUM, ZGAMMA, DRHYP, CGAMA, HYPGEO, HYPDRV,
HYPSER, ODEINT, BSSTEP, MMID, PZEXTR
Usage:
------
ZFUNC = ZHYPG2(ZA,ZC,ZZ,NMAX,EPS)
INPUT: ZA, ZC, ZZ, NMAX, EPS:
ZA - double complex number, contains value of parameter
. This type of calculations occurs in investigation
of the single and double ionizations by electron impact of two-nuclear
molecules (see papers [4,5]).
References:
-----------
1. Abramowitz M. and Stegun I. Handbook of mathematical functions,
National Bureau of Standards Applied Mathematics series. 55. 1964.
2. Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P.
Numerical recipes: The art of scientific computing.
Cambridge University Press, Cambridge, 1986.
3. Chuluunbaatar O. Bulletin of Tver State University:
Ser. Applied Mathematics. 2008, N = 26(86), pp. 47-64.
4. Chuluunbaatar O., Joulakian B.B., Tsookhuu Kh. and Vinitsky S.I.
J. Phys. B, 2004, v. 37, pp. 2607-2616.
5. Chuluunbaatar O., Joulakian B.B., Puzynin I.V., Tsookhuu Kh. and
Vinitsky S.I. J. Phys. B, 2008, v. 41, pp.015204-1-6.
Structure:
----------
FUNCTION
Name: ZHYPG2
Internal subroutines: ZSUM, ZGAMMA, DRHYP, CGAMA, HYPGEO, HYPDRV,
HYPSER, ODEINT, BSSTEP, MMID, PZEXTR
Usage:
------
ZFUNC = ZHYPG2(ZA,ZC,ZZ,NMAX,EPS)
INPUT: ZA, ZC, ZZ, NMAX, EPS:
ZA - double complex number, contains value of parameter  ZC - double complex number, contains value of parameter
ZC - double complex number, contains value of parameter 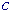 .
ZZ - double complex number, contains value of argument
.
ZZ - double complex number, contains value of argument 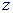 .
NMAX - integer number, the maximum number of summation of truncated
Gaussian series.
EPS - double precision number, given accuracy.
Sources with example and description are submitted.
Example:
.
NMAX - integer number, the maximum number of summation of truncated
Gaussian series.
EPS - double precision number, given accuracy.
Sources with example and description are submitted.
Example: